Ez az írásom négy évvel ezelőtt született. Mostanában újra fogalmazom, és picit tovább is fejlesztem, viszont közben rájöttem, hogy az új verzióban az eredeti szöveg sok értéke elvész. Ezért itt most megjelentetem ezt a régi írásomat. Az újabb verziót, amelyik több ponton azonos ezzel a korábbival, majd valamikor később, a jövőben publikálom. Ez a poszt mindenesetre szorosan kapcsolódik az előzőhöz. Azzal a kérdéssel függ össze, hogy mindaz, ami pusztán a modern, Galilei utáni fizika matematikai formalizmusából következik, mindaz vajon lehetséges-e? Ugyanis ez a matematikai formalizmus önmagában nem zárja ki, hogy az idő megforduljon, és visszafelé haladjon. Írásom a mellett érvel, hogy ezt a logika törvényei zárják ki. De figyelembe kell-e a logika törvényeit venni a fizikában? Sokan úgy vélik, a logikai-filozófiai megfontolások puszta előítéletek, nem kell velük komolyan foglalkozni, legalábbis a fizikában biztosan nem. Én nem így gondolom, ezért írtam meg az alábbiakat. Bizonyos további anomáliákra az újabb írásom fog kitérni.
* * *
Elméletileg utazhatnánk előre az időben, feltéve, hogy túléljük a gyorsulást. Beszállunk egy űrhajóba és nagyon gyorsan – több mint 100.000 km/sec sebességgel – távolodni kezdünk a Föld nevű bolygótól. Barátunk még jó utat kíván fénypostával. Nem ér el bennünket egy pillanat alatt az üzenet, mert a fénnyel összemérhető sebességgel utazunk. Amikor megérkezik a fényjel, milyen gyorsnak mérjük az űrhajónkban a fény terjedési sebességét? Mivel a fény terjedési sebessége 300.000 km/sec és a mi űrhajónk 100.000km/sec-el száguld amikor megérkezik a jel, talán arra gondolsz kedves olvasóm, hogy a fényt lassabbnak fogjuk mérni. Talán így gondolod: 300.000 – 100.000 = 200.000 km/sec. De ez tévedés, változatlanul 300.000 km/sec-et mérünk a száguldó űrhajón belül is. Hogyan lehetséges ez? Olyan módon, hogy a száguldó űrhajónak saját ideje van, és az lassabban telik, mint a mi földi időnk. Így aztán tovább gyorsítva az űrhajót, utazunk fél évet, de amikor visszatérünk a Földre, ötven év telt el, és egy új világba érkezünk. Kezet foguk a velünk egyidős unokáinkkal. Különös dolog ez, de nem lehetetlen.[1] De ha mehetünk előre az időben, akkor miért ne mehetnénk hátra? Azért nem mehetünk hátra, mert megtiltja a logika. Ugyanis lehetetlen úgy visszamenni az időben, hogy ne változzon meg a múlt. Tegnap nem voltam a Margitszigeten. Beülök az időgépbe, visszamegyek a tegnapba és kiszállok a Margitszigeten. Most akkor igaz vagy hamis, hogy én tegnap nem voltam a Margitszigeten? Ráadásul egy hét múlva visszajöhetek a mai napra, és megváltoztatom a mát. A mai nap mégsem utazom vissza a tegnapi napra a Margitszigetre. Aztán egy év múlva az időgéppel megint visszautazom a tegnapi Margitszigetre. Világos, ha megengedhető az időutazás, azaz lehet visszafelé menni az időben, akkor egész egyszerűen az állítások egy részének nem lesz meghatározott – azaz időtlen – igazságértéke, márpedig ez a logika összeomlását jelentené. De mi van, ha elkerülte valami a figyelmemet? Vegyük csak alaposabban fontolóra az egészet. Egyszerűsítsük le a problémát amennyire csak lehet úgy, hogy a lényeg azért megmaradjon. Használjunk modellt.
Nemrégiben volt a neten egy vicces videó ahol az emberek visszafelé mentek a járdán. Valahogy így képzeljük el ha megfordulna az idő, és visszafelé folyna. Bedobom a kávémba a kockacukrot, az föloldódik, majd különös villanást látok, zúgni kezd a fejem, távoli fény villog az éjszakában és lőn: ahogy ülők a kávém előtt, a kockacukor a kávéban ismét összeáll.
Engem a második jelenés lepne meg jobban, de még ott sem lennék teljesen biztos abban, hogy visszafelé folyik az idő. Inkább arra gondolnék, hogy egy nagyon valószínűtlen jelenségnek, talán csodának vagyok a szemtanúja.
Egyedül az időgép győzne meg. Beszállok az időgépbe, rázkódom jó fél órát, és ott vagyok a Muhinál 1241-ben. A saját időmben fél óra telt el előre, a külső időben viszont 772 év hátra. A királyt keresem. Figyelmeztetni akarom, hogy ne ünnepeljen túl korán, újra támadni fognak a mongolok. De kinevetik a furcsa beszédemet, nem ért meg senki, tehetetlenül állok, majd eltűnök az éj leple alatt.
A fizikusok közül sokan úgy vélik, hogy minden fizikai esemény lehetséges, amit nem zárnak ki fizikai törvények. Ezért aztán némelyek szerint nem kizárt, hogy az idő adott esetben visszafelé folyjék. A filozófusok közül egy híres gondolatmenet David Lewisé:[2]
Lewis gondolatmenete többek között a lehetséges világok feltételezésén alapul, amiben én nem hiszek, így ezzel most nem foglalkozom. Szerintem az időben való visszatérés lehetősége attól függ, hogy milyen egyéb előfeltevéseink vannak a világról. Látni fogjuk, hogy a fizikai tárgyakra vonatkozó azonosak megkülönböztethetetlensége, a fizikai tárgyak világvonala folytonossága és folyamatossága, valamint egy felső határsebesség létezése döntenek a kérdésben. Csak azt fogom megvizsgálni, hogy mit jelent az, hogy visszafelé folyik az idő, az időutazást meghagyom a scifi íróknak.
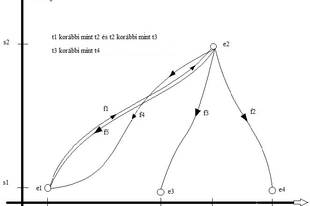
Legyen a mi világunk, amit mint modellt tanulmányozni fogunk, egy piciny egydimenziós világ, amelyben s1 és s2 pontok távolsága behatárolja a teret. Az idő t1 időpontban kezdődik és t4-ben ér véget, és ebben a világban csak egyetlen dolog van, amely dolognak csak egyetlen tulajdonsága létezik, nevezetesen az, hogy minden időpontban van valahol. Kicsit egyszerűbb ez a modell mint a mi világunk, amiben kétségtelenül több mint egy dolog van, de ez nem fontos. Mind a modellben, mind a mi világunkban csak véges sok dolog van, mindkettőben van tér és idő, és mindkettőben vannak olyan dolgok, melyek létezése azt jelenti, hogy valami van valahol valamikor. A modellben az ősrobbanás eseményét e1 jelöli, mikoris a világban lévő P objektum t1 időpontban s1 helyen volt. A világvégét e4 esemény jelöli, utána már nem történik semmi. Megfogalmazhatnánk természeti törvényeket is a modellben, pl. rögzíthetnénk egy maximális sebességet, vagy egyszerűsíthetnénk a modellt azzal, hogy diszkrét időben és atomos természetű térben képzeljük el az objektum mozgását. Ebben a piciny világ modellben P objektum története számos módon alakulhat. Igen, még ennek a nagyon kicsit világnak is nagyon sokfajta története lehet. Lássunk ezek közül pár érdekeset.
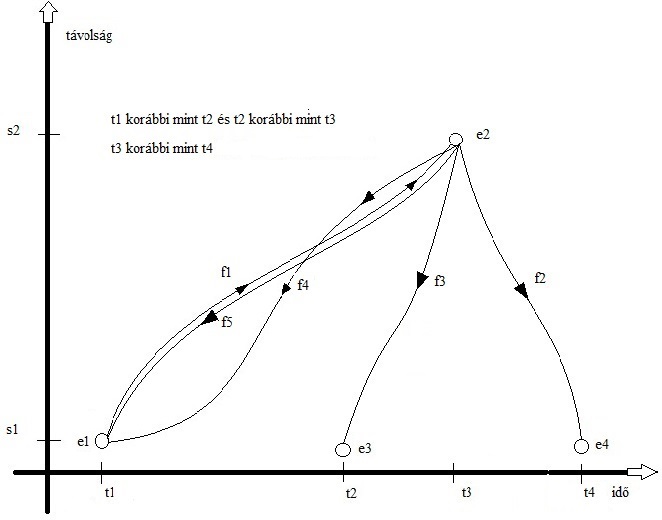
- Elindul P objektum f1 függvény mentén amíg s2-be ér. Ottan visszafordul, és valamivel gyorsabban f2 függvény szerint visszatér a kezdőpontba. Világos? Remélem nem. Nem mondtam meg mit jelentenek a nyilak. A távolság tengelyen a nyíl azt jelenti, hogy a nyíl irányában nő a távolság, az idő tengely esetén a nyíl azt jelenti, hogy abban az irányban ábrázoltam a jövőt. Ez talán nem újdonság, de miért rajzoltam nyilakat az f1 és f2 függvényekre? Azért, mert ezzel ábrázoltam, hogy P objektum előre vagy hátra halad az időben. A nyíl mutatja f1-n és f2-n, hogy a P az időben párhuzamosan halad az idő tengely nyilával, azaz az időben előre megy. Ha föltételezzük, hogy az idő csak előre folyhat, akkor a függvényekre tökéletesen fölösleges nyilat rajzolni. Ez nagyon lényeges megfigyelés. Ebben a lehetséges történetben P objektum minden időpillanatban van valahol és csak egyetlen helyen van egyszerre. A pont elindul és célba ér, de közben nem találkozik semmivel, főleg nem saját magával. Az útja végig folyamatos, bár az e2 eseményhez tartozó t2 időpontban olyan gyorsan vált útirányt, hogy abban a pillanatban nem értelmezett a sebessége. Nem sokszorozódik meg, csak egyetlen önmagával azonos példányban létezik. Nem így a következő esetben.
- P elindul f1 függvény mentén amíg s2-be ér. Ottan visszafordul a térben, és pontosan azzal a sebességgel ahogy odaért, visszafordul az időben is, és visszatér s1-be. Ezt ábrázolja f5 függvény, amit kissé távolabb rajzoltam f1-től hogy jobban látszódjon, de ez nem tévesszen meg. f1 az előre út, f5 a visszaút, melyek között csak annyi a különbség, hogy f1 esetén előre, f5 esetén visszafelé folyik az idő. Itt már óhatatlanul szükséges, hogy nyilakat biggyesszek a függvényekre, különben nem tudnánk, hogy melyik mutatja az előre, és melyik a hátra utat. Ha pontosan egymásra rajzoltam volna f1és f5 függvényeket, akkor nem is tudtam volna ábrázolni a két függvényt, mert csak egyet látnánk. Figyeljük meg jól f1 és az időben visszafelé utat ábrázoló f5 függvényeket. Vajon mit lát P objektum miközben f1 függvény szerint s1 pontból s2 pont felé halad? Furcsa élményben van része. Miközben halad előre az időben, folyamatosan találkozik saját magával, amint saját maga visszafelé jön az időben. Ráadásul egyazon helyen ott van P amint előre megy az időben, és ott van még egyszer amint épp visszafelé tér az időben az s1 pont irányába. Minden helyen minden időben egyszerre két dolog van, ami ugyanakkor azonos saját magával. Lehetséges ez egyáltalán? Lássuk a következő lehetséges történetét ennek a piciny világnak.
- Elindul P objektum f1 függvény mentén amíg s2-be ér. Ottan visszafordul, és f4 függvény szerint más sebességgel tér vissza a kiinduló pontba. Bizony most is feltétlenül szükségesek a nyilak. Az egyedüli lehetőség a nyilak elkerülésére az volna, ha az időnek több dimenzióját is ábrázolnám, és a visszafelé folyó időt egy másik idő dimenzió fejezné ki.
Amennyiben a visszafelé folyó időt egy másik idődimenzióhoz kötném, akkor kérdéses, hogy mi módon ábrázoljam amikor az objektum ismét előre halad az időben? Egyetlen objektum esetén megoldást jelentene, hogy az idő folyásának minden irányváltásához egy újabb dimenziót rendelek, és így több dimenzió fog tartozni mind az előre, mind a visszafelé folyó időhöz. Ezzel a javaslattal azonban az a baj, hogy nem működik több objektum esetén, amikor az objektumok egyazon idő dimenzióban mozognak, de nem egyformán haladnak előre vagy hátra az időben.
Figyeljük meg, hogy f1 és f4 függvény egy pontban metszi egymás. Mit ábrázol ez? Azt ábrázolja, hogy ott van egy esemény, ahol egyazon időben egyazon helyen találkozik az előre menő objektum saját magával amint éppen visszafelé halad. Mi a helyzet a többi időpontban? Ott is egyszerre két P objektum van. Az egyik éppen előre halad az időben, a másik meg jön vissza, de szerencsére legalább a helyük különbözik. Ez azonban ellentmond az azonosság törvényének, mivel van két azonos objektumunk különböző tér-idő jellemzőkkel. Emlékszünk, hogy a korábbi f1 és f5 pályákon furcsa helyzet van. Mindvégig ott van P is amint előre halad, és állandóan találkozik saját magával amint visszafelé megy. Végül tekintsünk egy újabb lehetséges történetet.
- P objektum elindul f1 szerint s1 ből s2 irányába, majd miután célba ért, valamivel gyorsabban elindul visszafelé az időben egészen addig, amíg s1 kiindulási helyzetbe ér. Az elindulás után, azaz t1 időpont után semmi különöset nem lát, magányosan halad t2 időpontig. Akkor viszont valami furcsa történik vele. Egyszerre meglátja saját magát a háta mögött a kiindulási helyzetben, s1 helyen, amint odaért saját maga visszafelé haladva az időben. Ezek után P objektum folyamatosan látja saját magát a háta mögött amint egyre közeledik s2-höz, végül t3 időpontban összefut saját magával e2 eseményben, amikor is önmagára találván a megkettőzött P objektumból egyetlen P objektum lesz ismét. Itt ismét az azonosság törvénye megsértésével állunk szemben.
Azért meséltem el ezt az egészet, hogy megvilágítsam, mit is jelent, ha az idő visszafelé folyik. Így jobban megérthetjük mi az ami kizárja ebben a piciny világban az idő visszafelé folyását, és talán a mi nagyobb világunkban is hasonló dolgok tiltják meg az idő visszafelé folyását. Vagy épp ellenkezőleg. Ha feltételezzük, hogy a mikrofizikai jelenségek világában az időben visszafelé is haladhat egy elektron, akkor az előbbi példa segít megérteni, hogy mit tapasztalnánk. Pl. az időben visszafelé haladó elektront pozitív töltésűnek látnánk, tehát az tapasztalnánk, hogy vannak pozitív töltésű elektronok. De ezek tényleg vannak, akkor most némelykor visszafelé folyik az idő? Attól függ. Ha úgy véljük vannak negatív és vannak pozitív töltésű elektronok, akkor nem kell hinnünk az idő visszafelé folyásában. Viszont úgy is gondolkozhatunk, hogy csak negatív töltésű elektronok vannak, melyek néha visszafelé mennek az időben, és ezeket tapasztaljuk a saját időnkben pozitron gyanánt.
Térjünk vissza a mi kis modellünkhöz. Mi tiltaná meg az időben visszafelé való haladást a modellben? Semmi nem tiltaná meg, hogy a modellben egy lehetséges világban visszafelé folyjon az idő, feltéve hogy az objektum csak visszafelé halad az időben. Viszont az objektum egy ideig az idő egyik majd a másik irányába való haladását megtilthatják bizonyos kikötések. Tehát az objektum nem haladhat egy ideig előre az időben, majd visszafelé az időben egyazon lehetséges világban. Ezeket a tiltások veszem sorra az alábbiakban. Abból indulok ki, hogy az objektum először előre halad az időben, és azt vizsgálom, minek mondana ellent, ha utána visszafelé haladna az időben. Sorra veszem a korábban bemutatott (1), (2), (3), (4) lehetséges történeteit a modellnek.
(i) 1. lehetséges történet az időben előre zajlik. Az egyedüli furcsaság, e2 esemény, mikoris az objektumnak nem meghatározott a sebessége. Azért nincs sebessége az objektumnak t3 időpontban, mert ott törés van a pályájában, azaz t3 időpontban az objektum út-idő pályája nem differenciálható. Egyszerűen fogalmazva, a pályának nincs érintője t3 időpontban. Ha kikötnénk, hogy a modell világában van egy véges maximális sebesség, akkor ez kizárná az objektum 1. történetét, és az összes többit is, mivel abban is ilyen éles törést tartalmaz az objektum út-idő függvénye, másképpen mondva világvonala.
(ii) 2.-t tiltja, ha egyazon tér-időben csak egyetlen P lehet.
(iii) 3.-t tiltja (ii) vagy hogy P egyazon időpontban nem lehet egyszerre két helyen.
(iiii)4.-t tiltja (iii) vagy hogy P csak fokozatosan haladhat és nem tűnhet elő hirtelen a semmiből. Ha kikötjük, hogy az objektum kizárólag folyamatosan haladhat és sebessége soha nem lehet végtelen, akkor lehetetlen, hogy az objektum visszaforduljon az időben. Utóbbi kikötés tehát nem az időben visszafelé haladást tiltja meg, hanem az előre és visszafelé haladást egyszerre, egyazon lehetséges világban.
(ii), (iii), (iiii) kikötések a dolgok téridőben való önazonosságával kapcsolatosak. Ha megengedjük az idő visszafelé folyását, akkor a dolgok egyszerre több helyen is létezhetnek egyazon időpontban, hirtelen megváltoztathatják a helyüket, és megsokszorozhatódhatnak a tér- időben. Különös világ lenne egy ilyen világ. Ebben biztosan nem lennének érvényesek a fizikai tárgyak önazonosságára vonatkozó mindennapi feltevések. De ha felfüggesztjük a józan ész föltevéseit és megengedjük az idő visszafelé folyását, akkor semmi sem zárja ki az alábbi „egydimenziós féreglyukak” létezését sem:
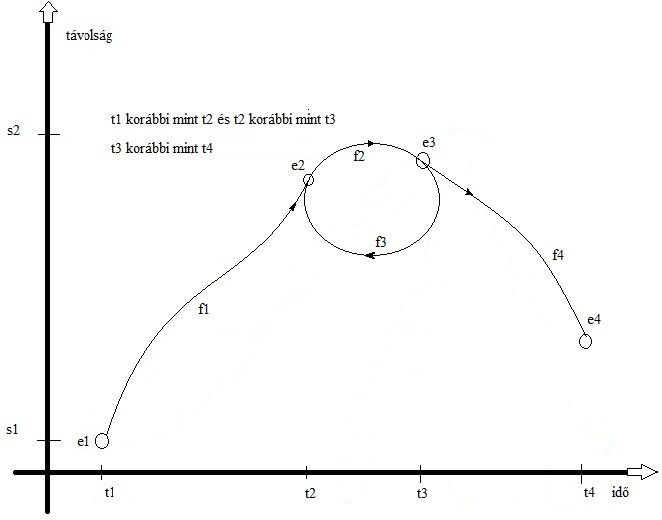
Figyeljük meg mi itt a lényeg. Az f1 és f4 világvonalakkal semmi gond, ezek normálisak, mert az időben előre haladnak. Viszont a t2 – t3 időtartományban, melyeket e2 és e3 események határolnak, a P objektum egyazon időben odafelé az egyik helyen, visszafelé egy másik helyen van, és ki tudja hányszor jár körbe, amíg végre elér az e4 eseményhez. Ha jól megfigyeljük pl. t3 után egy rövid ideig három önmagával azonos, de mégis különböző helyű P objektumunk van. Figyeljük meg azt is, hogy az időben visszaforduló majd utána előre haladó objektum kétszer egy pillanatra végtelen sebességgel halad. A végtelen sebesség ellentmond a relativitáselméletnek. Hogyan lehetséges ez logikai ellentmondás nélkül? Nem tudom, de esetleg van rá megoldás. Talán épp ezért ilyen különös az elemi részek világa.
Richard Phillips Feynman írja a „QED A megszilárdult fény” c. népszerű tudományos könyvében:
„Még különösebb eset (c), amikor az elektron kibocsát egy fotont, majd visszafelé halad az időben, hogy elnyelhessen egy másikat, és aztán újra az idő természetes folyásának megfelelően mozog előre. Az ilyen „visszafelé mozgó” elektron útja olyan hosszú is lehet, hogy igazinak tűnik a laboratóriumban elvégzett kísérletben. … Ha az időben visszafelé mozgó elektront az idő normális irányában vizsgáljuk, akkor az elektron teljesen ugyanolyan, mint egy hétköznapi elektron, azzal a különbséggel, hogy ez az elektron vonzza a normális elektront – erre azt szoktuk mondani, hogy „pozitív töltésű”. … A fenti jelenség általános a természetben. Minden részecske tud valamennyi ideig valamekkora amplitúdóval visszafelé mozogni az időben, így minden részecskének van antirészecskéje.”[3]
Feynman a „Fizikai törvények jellege” c. szintén a nagyközönségnek írt korábbi könyvében még nem ebben a szellemben tárgyalja a múlt és jövő problémáját. Ottan az entrópia fogalmával magyarázza az idő irányát. Viszont egy olyan modellben, ahol csak egyetlen objektum van nem értelmezhető az entrópia, így nem biztos hogy ellentmondás van a korábbi és az újabb álláspontja között.[4]
Összefoglalás
Egyszerű modellünkben ahol mind a tér mind az idő egydimenziós, egy időben visszafelé haladó objektum feltételezése ellentmond a relativitáselméletnek és ellentmond az önazonosság logikai törvényének is.
Az előbbit kikerülhetjük a tér és idő atomos természetének feltételezésével, valamint azzal, hogy a modellbeli objektum egy atomnyi idő (ütem) alatt legfennebb egy atomnyi távolságot haladhat. Ekkor az objektum pályája mindenképpen folyamatos lesz a diszkrét időben és szükségszerűen nem halad gyorsabban a diszkrét tér-idő által maghatározott maximális sebességnél. Ugyanakkor a tér-idő atomos természetének föltételezése két vagy több dimenzióban nehéz, vagy egyenesen megoldhatatlan geometriai problémákat vet fel.
Utóbbit – a logikának való ellentmondást – csak úgy kerülhetjük ki, ha a modellben mozgó dolgokat nem egyetlen fizikai tárgynak (objektumnak), hanem egy tárgy instanciájának tekintjük. Ekkor azonban a pályák sem a fizikai tárgy világvonalait ábrázolják, hanem a tárgyak példányainak világvonalait. Ekkor eltűnik a modellből a valóságos fizikai tárgy és nem is tudunk mondani semmit annak a történetéről, hanem csak az instanciái történetéről.
[1] A dolog azért nem ilyen egyszerű. Hraskó Péter írja „A relativitáselmélet alapjai” c. könyvében: „Azonban van itt egy probléma: Az idődilatáció – mint tudjuk – szimmetrikus, és ebből arra gondolunk, hogy akkor az otthon maradt testvérnek is fiatalabbnak kell lennie, mint annak, amelyik elutazott, ami nyilvánvalóan lehetetlen, ha ikerparadoxon létezik . … Az ellentmondás azért szűnik mégis meg, mert …. az utazó testvér vonatkoztatási rendszere ugyanis nem inerciarendszer …” (2009) Typotex kiadó, Bp., p. 32.
[2] The paradoxes of time travel, American Philosophical Quarterly, April 1976, pp.145-152. Letölthető a netről: http://www.csus.edu/indiv/m/merlinos/Paradoxes%20of%20Time%20Travel.pdf
[3] Richard Phillips Feynman, QED A megszilárdult fény (2003) Scolar kiadó, ford. Alföldy Bálint, pp.9-98. Eredeti kidás: QED The Strange Theory of Light and Matter, Princeton University Press (1988) Princeton, New Jersey
[4] Richard Phillips Feynman, A fizikai törvények jellege (2005) Akkord kiadó