Bevezetés

Alább összefoglalom és kiegészítem azokat a gondolatokat, amiket korábbi írásaimban elszórtan a szabad akaratról mondtam.

A szabad akarat, mint filozófiai fogalom, mint filozófiai probléma szorosan kapcsolódik néhány másik kérdéshez, amelyeket szintén tárgyaltam más írásaimban, de most a lényegesebb részeiket ide másolom, mert ezek nélkül nem érthető az álláspontom.[1] Ilyen kérdés a logikai és a fizikai determinizmus fogalmi különbségének világos megkülönböztetése. Ezek tisztázása után, amit védelmezni fogok, azt kompatibilizmusnak nevezik a filozófiában.[2] Rudolf Carnap 1962-ben Minnesotában részt vett a „The nature of causality and probability” c. konferencián, ahol meggyőzően érvelt a szabadság, szabad akarat egy kompatibilista felfogása mellett, rámutatva, hogy a természeti törvényeket kategória hiba külső kényszerekként értelmezni. Mindenben egyetértek Carnap gondolataival, az én gondolatmenetem azonban oda konkludál, hogy, a kompatibilista álláspontot óvatosan kell megfogalmazni, mert bármilyen meggyőző, nem lehet univerzális, nem vonatkozhat önmagára. (Ez egyébként más filozófiai problémákra, mint pl. a fizikalizmus is érvényes.) Csak így szólhat: tinektek nincsen szabad akaratotok a szó filozófiai értelmében, mert anyagi rendszerek vagytok, és az elmétek csak terméke az agyműködéseteknek, de nekem, aki hozzátok beszélek, szabad elmém van, melyet a saját gondolatai vezérelnek. Természetesen ezt a másik ember épp így elmondhatja rólam.  De ha önmagára vonatkozik, akkor ez az álláspont eliminálja az igazság fogalmát azzal, hogy redukálja az elmét a fizikai működésre, így ezért önmaga igazságát is megsemmisíti. Tehát az agyműködéstől független elme, és filozófiai értelemben vett szabad akarat, egy munkahipotézis, melynek logikai okai vannak, és nem metafizikai.

1. A logikai determinizmus igazsága

Képzeld el, hogy a világ egyetlen pénzérméből áll, annak is csak két állapota lehet, fej vagy írás, és ez a világ összesen három pillanatig létezik. Keletkezik, van, majd eljön az utolsó pillanat. Teljesen mindegy hogy ebben a világban létezik-e valamilyen természeti törvény, ami kiszámíthatóvá teszi, vagy valószínűsíti, az érme következő állapotát, vagy sem. Az érme összes lehetséges történte ettől függetlenül meghatározott az alábbi módon:

1. fej fej fej; 2. fej fej írás; 3. fej írás fej; 4. fej írás írás; 5. írás fej fej; 6. írás fej írás; 7. írás írás fej; 8. írás írás írás

Bárhogy dobod föl háromszor a pénzérmét, a valóság ott lesz a fenti sorozatok között. Ugyanakkor ama tény, hogy a nyolc sorozat között szükségszerűen ott van a ténylegesen megvalósuló is, fizikailag nem határozza meg, hogy mi fog történni. És ami igaz a pénzérmére, igaz az emberi életekre is. A logikai determinizmus matematikai szükségszerűség és nem fizikai. Kicsit jobban elmagyarázom.

Osszuk be a Föld felszíne feletti és alatti 11000 km-es véges tartományt kicsiny kockákra. Nyilván csak véges sok kockát kapunk, és a kockákat egyértelműen azonosíthatjuk egész számokkal. Minden ember élete minden időpontjához hozzárendeljük a személy tömegközéppontja által elfoglalt hely számát – azt a kockát ahol éppen tartózkodik. Így az összes valaha élt és a jövőben élő ember életéhez egyértelműen hozzárendelhető egy olyan függvény, amely megadja, hogy az illető mely időpontban mely helyen tartózkodott. Vegyük most a Föld véges élettartamához tartozó összes lehetséges ilyen függvényt. Ezek a függvények olyanok lesznek, hogy diszkrét időt feltételezve a szomszédos időpontokhoz tartozó térkockák érintkezni fognak egymással. (Ez azért van így, mert a folytonos világban a mechanikai mozgást differenciálható függvények írják le.) Ezekből a diszkrét függvényekből csak véges sok lesz, és miden egyes ember valóságos életének megfelel ebből legalább egy, amelyik kellő pontossággal leírja élete pályáját. Nem ismerjük ezeket a függvényeket, nem tudjuk, hogy melyik emberhez melyik függvény tartozik, de az logikailag szükségszerű igazság, hogy az imént meghatározott függvények közül minden emberhez tartozik legalább egy, amelyik leírja az ő életét. Ha építünk egy nagy számítógépet, amelyik tartalmazza mindezeket a függvényeket, akkor az tartalmazni fogja a jövő egy részleges leírását is. Tartalmazni fogja az összes ember térbeli életpályáját. Csak részlegesen tudjuk melyik írja le a mi életünket, de ott lesz közöttünk az én és a te életed is, a jövő is ami reád vár. Ott lesz az összes valaha élt emberé, Julius Caesaré és az összes rabszolgáé, és mindazoké, akik eddig éltek vagy a jövőben éli fognak. Ha mindezt négydimenziós térben ábrázoljuk, akkor megkapjuk, hogy egyáltalán mely emberek találkozhatnak, szerethetik vagy gyűlölhetik egymást, szólhatnak egymáshoz, vagy fordíthatják el a tekintetüket.

Ami igaz az életed során elfoglalt helyekre, igaz minden egyéb tulajdonságodra is. Megalapozottan feltételezhetjük, hogy tulajdonságaid száma véges, így az előbbi példa alapján megszerkeszthető az összes tulajdonságod összes lehetséges időbeli függvénye is. Ebből legalább lesz egy, amelyik megfelel a tényleges életednek. Ha ezt beláttuk, akkor csak egy lépés annak a fölismerése, hogy az életedet leíró függvények halmaza meghatározza az életedet leíró valamennyi állítás igazságértékét. Adott tehát azon mondatok halmaza, melyek életed tényeit írják le, bár nem ismered ezek java részét. Ez azonban mellékes, életed jövőbeli tényei léteznek, csak ismeretlenek előtted.

Bertrand Russell ezt a példát az egész világra kiterjesztve fogalmazta meg, mint annak bizonyítékát, hogy „ahogy lesz, úgy lesz”– Quine így nevezte ezt az érvet.[3] Russell így fogalmazott anno:

„Ha a megengedett formulák bonyolultságának a foka tetszőlegesen nagy lehet, akkor – úgy tetszik – minden rendszernek melynek egy adott pillanatban vett állapota bizonyos mérhető mennyiségek függvénye, determinisztikus rendszernek kell lennie. Illusztrációként tekintsünk egyetlen anyagi részecskét, amelynek koordinátái t időpontban legyenek x_t, y_t és z_t. Ekkor bárhogy mozog is a részecske, elméletileg kell lennie olyan f₁, f₂, f₃ függvényeknek, hogy x_t=f₁(t), y_t=f₂(t), z_t=f₃(t). Következésképpen elvileg lehetségesnek kell lennie annak, hogy az anyagi világegyetem t időpontban vett egész állapotát t függvényeként ábrázoljuk.”[4]

Mindezek alapján értelmezhetjük a klasszikus logika olyan felfogását – így gondolkodott Ruzsa Imre is – hogy a perfekt mondatoknak, melyeknek egyértelmű információ tartalma van, egyaránt örök, változatlan igazságértéke van, függetlenül attól, hogy a múltra, a jelenre, vagy a jövőre vonatkoznak. Az igazságértéküket a Russell által említett, világ-leíró függvény határozza meg, melyet csak részben ismerünk, de biztosan létezik. Hogy minden kijelentésnek van igazságértéke, a logika belső elméleti feltevése, mint pl. a valós számok léte a matematikában, nem szükséges ezt, mint külső állítást névértéken venni.

De vehetjük névértéken is ezt a felfogást, mint külső, metafizikai állítást. Nagyon sok filozófus úgy gondolja, hogy a klasszikus logika ilyen felfogása, miszerint az igazság időtlen tulajdonság, problematikus, nyugtalanító. Ha az igazság időtlen tulajdonság, és a jövőre vonatkozó állításoknak is van igazságértéke, akkor már most a jelenben is van igazságértéke. Ha van igazságértéke, akkor léteznie kell annak, ami megalapozza azt az igazság értéket. A tények alapozzák meg az igazságértéket, következésképpen már most a jelenben léteznie kell a jövőbeli tényeknek. Ha a jövőre vonatkozó állításoknak már a jelenben is van igazságértéke – vélik sokan – akkor a jövő megváltoztathatatlan, mert eleve eldöntött, nincsenek alternatívák. Ahogy lesz, úgy lesz. Ez fatalizmust jelent, mert az eleve elrendeltség következik belőle. A dolog azonban nem ilyen egyszerű. A jövőbeli propozíciók igazságértékét alapozhatjuk arra a függvényre, amit Russell említ, ami leírja a jövőt. Nem ismerjük ezt a függvényt, de biztosan létezik, egy a sok közül. Ennyi a logikai determinizmus igazsága. A függvény azonban nem fizikai tárgy vagy fizikai esemény. A függvény létéből nem következik az események eternalista felfogása. Hihetünk az események eternalista felfogásában, ha más megfontolásból vonzónak találjuk, azaz elfogadhatunk valamilyen tény ontológiát/metafizikát, és akkor valóban a fatalizmus egyfajta igazolását adjuk, de ez nem elkerülhetetlen, másképp is gondolkozhatunk. Ha mégis elfogadjuk, akkor azonban a jövőbeli tények nem fizikai eseményekként okai a jövőnek, hanem logikai megalapozói a jövőre vonatkozó kijelentések igazságának. Igazság alkotók, de nem okok.

2. Determinizmus és véletlen

Milyen lenne egy kaotikus, vagy ellenkezőleg egy determinisztikus, avagy a kettő közötti részben determinisztikus (valószínűségi) világ? Bemutatom néhány csak a filozófiai lényegre összpontosító példán. Ezekben a mikro-világokban is vannak dolgok, melyek a tér és idő különböző pontjait foglalják el.  Van ezeknek a világoknak természete: a benne lévő objektum folyamatosan létezik az időben, mindig van valahol, és egyszerre csak egy helyen van. Mozgását vagy a véletlen, vagy valószínűségi, vagy determinisztikus törvények határozzák meg. Ezekben a mikrovilágokban is vannak dolgok, melyek a tér és idő különböző pontjait foglalják el. Van ezeknek a mikro-világoknak természete: a benne lévő objektum folyamatosan létezik az időben, mindig van valahol, és egyszerre csak egy helyen van. Mozgását vagy a véletlen, vagy valószínűségi, vagy determinisztikus törvények határozzák meg. A tudomány, különösen a fizika, kémia, modelleket használ. Mivel számomra ez a minta, én is modellek segítségével mutatom be álláspontomat.

2.1 Forgalmi káosz

Forgalmas útkereszteződésben állunk, hömpölyög az autók áradata. Minden rendben van, az autók hol az egyik, hol a másik irányban haladnak. A járművek haladása rendezett sorokban történik, előrelátható, hogy mikor áll meg az egyik irány és mikor indul a másik. A forgalomirányítás modelljében gondolkozva rend van a kereszteződésben. Most hirtelen elromlanak a közlekedési lámpák. Néhány autó bennragad a kereszteződésben, mások össze vissza hajtanak. A becsatlakozó utcákon néhány perc alatt torlódás jön létre, zűrzavar keletkezik. Megszűnt a rend a közlekedési szabályok nézőpontjából – egy adott modellből nézve – de a járművek fizikájának a szintjén, fizikai modellel szemlélve az eseményeket megmaradt a szabályszerű viselkedés. Mindkét esetben biztosak vagyunk benne, hogy az autók mozgása megmagyarázható. Mindkét esetben hiszünk abban, hogy a járművek mozgásának mindig volt oka, és ezekben az okokban pedig azért hiszünk, mert úgy véljük a kaotikus esetben is szabályoknak megfelelően történik minden, csak ezeket az egyedi szabályokat nem szervezi egységbe a jelzőlámpák működése. Nem változtak meg a fizika törvényei, és a motorok, kerekek, fékek és lámpák viselkedése továbbra sem mond ellent a fizika törvényeinek. A vezetők is tudják merre akarnak menni, és ilyen módon minden mozgás – a zavaros is – megmagyarázható, csak ez a magyarázat jóval bonyolultabb a második esetben, mint az elsőben, amikor még jól működtek a jelzőlámpák. Ez a példa érzékletesen mutatja, hogy egy jelenség bonyolult, emberi szempontból szabálytalan mivolta önmagában nem alapozza meg azt, hogy nincsenek a mélyében érvényben olyan másfajta szabályszerűségek, amelyek magyarázatul szolgálnak arra ami történik. A szabályszerűségek és okok megtalálása attól függ, hogy milyen modellel kívánjuk megmagyarázni az eseményeket. A választott modelltől függ, hogy van-e szabályszerűség és mi az ok. E közlekedésről szóló példa ugyan szemléletes, mert a mindennapi életből vett ismert jelenség, de nem elég elvont, és túlságosan összetett, sok részletkérdés vonja el a lényegről a figyelmünket. Nem tudjuk egyszerű matematikai eszközökkel leírni ami történik, így filozófiai vizsgálódás céljára kevésbé tanulságos. Lássunk egy jobb példát.

2.2 Háromszögbe zárt világ

Képzeljünk el egy egyenlő oldalú háromszöget melynek minden oldala egységnyi hosszúságú, és három oldalának nevei: A,B,C. Ekkor a háromszög kerületének minden egyes pontját egyértelműen meghatározhatjuk úgy, hogy A és C találkozási pontjából kiindulva B irányába kijelölünk egy haladási irányt, így minden oldalnak lesz eleje és vége. Az oldalak elejéhez 0, a végükhöz 1 számot rendelünk, és a közbenső helyeket is arányosan értelmezzük. (Nem mondom, hogy elnevezzük, mert nincs annyi név ahány valós szám van.[5]) Az A-hoz tartozó számokhoz nullát, a B-hez tartozó számokhoz 1-et, míg a C-hez tartozó számokhoz 2-t adunk hozzá. A háromszög kerületének összes pontja így a nulla és három tartományba fog esni. Legyen három ilyen háromszögünk, és mindegyikben pattogjon egy pont vagy parányi kör vég nélkül. Diszkrét időskálán képzeljük el a pont mozgását, és csak arra figyelünk, csak azt értelmezzük, amikor a pont a háromszög egyik oldalán van. Azzal nem foglalkozunk, hogy miképp és mennyi idő alatt ér oda a pont. Föltételezzük, hogy minden esetben egy diszkrét időegységnyi idő alatt érkezik a következő helyre a pont. Ezek pályáját a háromszögekben három különféle szabály határozza meg. Az első háromszögben ha a pont valahol van, akkor a következő oldalba való becsapódás helye egyforma valószínűséggel bármelyik pontja lehet a háromszög oldalának, még az is előfordulhat, hogy egyhelyben marad a pont. A második háromszögben a pont valamelyik oldalba való becsapódási szöge megegyezik a visszaverődés szögével. A harmadik eset a másodikhoz hasonlít azzal az eltéréssel, hogy a visszaverődési szög nincs pontosan meghatározva, csak annyi biztos, hogy a visszaverődő pont iránya két szélső érték közé esik, de hogy melyik lesz a két szélső érték között a tényleges visszaverődés szöge, arra nincs szabály, az véletlenül következik be.

Ezt mutatják az alábbi ábrák.

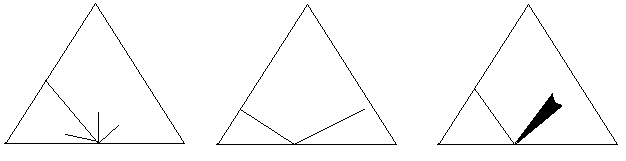
2. ábra

Érdemes lenne azt is megvizsgálni, miképp változna a modell, ha több, esetleg nagyon sok parányi kör pattogna a háromszögekben, és azok a háromszögen belül egymással is ütközhetnének, esetleg vonzanák, vagy taszítanák egymást, vagy másképp hatnának egymásra? Miképp változna a modell ha háromszög helyett gömböt választanánk, és az objektumok nem két dimenzióban, hanem háromban (vagy többen) mozognának, és a gömb tágulna? Ezen kérdések megválaszolása komplikált matematikai apparátust igényel, ezért én most tovább egyszerűsítem a modelleket.

Matematikai nézőpontból másodlagos, hogy a pont helyei egy háromszög oldalain helyezkednek el vagy egy egyenesen. A lényeges az, hogy a pont egy véges szakaszt ciklikusan bejár ahol az i+1-ik diszkrét időpontban elfoglalt helyét az i-ik időpontban lévő helye határozza meg valamilyen függvény által. Vegyük a második háromszöget, ahol a pont pályája egyértelműen meghatározott. Feltéve, hogy a szakasz folytonos, több filozófiai kérdés is fölmerül bennünk:

(a) Nyilván van olyan indulása a pontnak, hogy véges idő után kiindulási helyére tér vissza. De van-e olyan, hogy sohasem?

(b) Van-e olyan indulása a pontnak, hogy végtelen idő alatt a háromszög kerületének összes pontját bejárja? Hány ilyen indulási pont van?

(c) Vajon miféle képességek, milyen eszközök kellenének ahhoz, hogy a pont helyét bármely későbbi időpontban előre lássuk?

(d) Tegyük fel, hogy a háromszög oldalai véges sok hely atomból állnak. Ilyen módon a három oldal összes hely atomjának egész számokat feleltethetünk meg. Mindhárom esetben a pont pattogása szám sorozatokat generál. Az első és a harmadik esetben ezeket a sorozatokat részben vagy teljesen a véletlen határozza meg. Kérdés azonban mit értsünk véletlen sorozat alatt ebben a két esetben? Egy kísérleti definíció a következő:

Véletlen sorozat := olyan végtelenek feltételezett sorozat, amelyik nem állítható elő végetlen idő alatt Turing géppel. Természetesen egy ilyen sorozat semmilyen véges determinisztikus modellel (automatával) sem generálható.

A determinisztikus esetben a pont bármely két egymás utáni helye egyértelműen meghatározza a következő helyét. Első lépésben tegyük fel, hogy csak egy pont mozog ciklikusan a véges szakaszon. Ha a pont helyei racionális számoknak felelnek meg, melyek tört formában ábrázolhatók, akkor egy végtelen képességű matematikus bármely későbbi időpontban meg tudja határozni a pont helyét formulákkal való számolással, viszont egy digitális számítógép amelyik már a racionális számokkal is kis hibával számol, erre nem képes. Azért nem, mert nem törtek, hanem számsorozatok alakjában ábrázolja a számokat. Pl. az ’1/7’ számnak egy végtelen számsorozat felel meg, aminek csak töredékét képes a számítógép ábrázolni (0.142857143). Ha a pont helyei valós számoknak felelnek meg, a gép akkor is csak rövid távon képes jó közelítéssel meghatározni a pont helyét. Ám ekkor már a korábban említett végtelen képességű matematikusnak is számok aktuális végtelen sorozataival kéne tökéletesen pontosan számolnia, ami csak úgy lehetséges, hogy ezekre a számokra egy-egy számjellel (pl. π) hivatkozik. Viszont egy ideális analóg automata képes lenne pontosan meghatározni a pont helyét bármely későbbi állapotban, csakhogy ideális analóg automata a fizikai valóságban nem létezik.

A második esetben vegyük azt a még mindig determinisztikus verziót, amikor nagyon sok egymással is ütköző kicsiny kör pattog. Az ütközések következményeit is egy determinisztikus szabály rögzíti. Analóg automatával ekkor is célt érhetünk, de a végtelen képességű matematikus valószínűleg elvileg megoldhatatlan problémák elé kerül, és a legkevesebbre a számítógépek képesek. A feladat tehát determinisztikus működést feltételezve az alábbi táblázat kitöltése:

1. táblázat

Nem-determinisztikus viselkedést feltételezve, legfeljebb csak rövidtávon, és csak adott hibával tudjuk megjósolni a pattogó pont, vagy körök helyét. Úgy tűnik ekkor nem fontos mi modellez – véges automata, Turing gép vagy analóg számítógép – a lehetőségek jobbak a nullánál, de korlátozottak.

2.3 Világok egy vonal mentén

Egyszerűbbé válik a példa, és könnyebben modellálható a filozófiai tartalom lényegének megőrzése mellett, ha a pont mindössze egy véges egyenes szakaszon halad. Annyival is legyen egyszerűbb a vizsgálódás, hogy a szakasz csak diszkrét helyekből, adott esetben 32 helyből álljon, 32 egymást követő természetes szám növekvő elrendezése szerint. Háromféle szabály alapján, három véges világot képzelünk el. Mindhárom véges világ 32 helyből áll, az idő is diszkrét, és egyetlen dolog van mindhárom világban, és az az egy dolog időnkét változtatja a helyét. Ezekben az egyszerű világokban lévő dolgoknak a helyük az egyetlen jellemzőjük. Az első esetben a pont bármelyik x helyet követő állapot után bármelyik másik y, vagy éppen azonos (x=y) helyre kerülhet. Így a számok tetszőleges véletlen sorozatát kapjuk. A második esetben a pont elindul a ’1’-jelnek megfelelő helyből, a következő hely ahova érkezik a ’2’ jel, majd a ’3’ jelhez jut, és így tovább egészen addig amíg az utolsó, a ’32’ jel által jelölt helyig elér. Ez után ismét a ’1’ helytől folytatja tovább az útját. A harmadik esetben a pont soha nem megy hátra, de nem megy előre többet, mint három egység. Mehet előre egy, kettő, három távolságegységet, vagy éppen semmit. Hogy pontosan mennyit megy előre az a véletlenen múlik. A három példa szemléletesen mutat három világot: egy teljesen kaotikusat, egy teljesen determinisztikusat, és egy részben determinisztikusat (valószínűségit). A második és harmadik világban érvényesek szükségszerű igazságok: pl. a pont soha nem megy hátra, és véges idő alatt eléri a végső helyzetét. Bizonyos szükségszerű állítás még az első, kaotikus világban is igaz: a pontnak minden időpontban van egy és csak egy helye, de a pont történetéről már semmiféle biztos előrelátással nem élhetünk. (Egy más bonyolultabb modellben, ahol a pont helye csak valószínűségi függvénnyel adott, a helyek statisztikai eloszlás függvény formáját öltik.) Nem tudjuk megadni minden esetben hogy mi fog történni, de bizonyos hogy le fogja írni a pont haladását egy függvény. Ennél több is igaz. Meghatározható azon függvények véges halmaza amely elemi között ott lesz a jövőt leíró függvény is. Ez a függvény pontosan leírja a jövendőt, de nem határozza meg azt. Annak köszönhetően, hogy ezek véges világok, mindhárom esetben ki is számolható az összes lehetséges függvény, másképp fogalmazva a pont véges idő alatti világtörténete 32 diszkrét időpontot feltételezve az alábbi szerint alakul. Az alábbi számok a lehetséges világtörténetek számát mutatják:

kaotikus világ: 45,671,926,166,590,700,000,000,000,000,000,000,000,000,000,000

determinisztikus világ: 1

valószínűségi világ: 4,611,686,018,427,390,000

A számok mutatják, hogy ezek lényegesen különböző világok, miközben az „ahogy lesz, úgy lesz” érv, mint cáfolhatatlan igazság, mindegyikükben érvényes. Két esetben nem tudjuk vagy nem tudjuk pontosan meghatározni a jövőt, a pont történetét, de azt mégis biztosan tudjuk, hogy létezik egy függvény ami leírja a jövőt, a pont eljövendő történetét. Az előző mondatban szereplő „létezik” szó az ami a filozófiai görcsöket okozza. Létezik a jövőt leíró függvény, de nem tudjuk előre melyik az, és két esetben nem is tudhatjuk. Ez a létezés alapozza meg, hogy mindhárom esetben minden jövőre vonatkozó állításnak van egyértelmű igazságértéke, csak nem tudjuk idő előtt, hogy mi az. Mégis van értelme az előreláthatatlanság és előreláthatóság értelmezésének és fokozatbeli megkülönböztetésének a második és harmadik példa alapján.

Figyeljük meg, hogy a teljesen determinisztikus modell esetén is igaz, hogy a pont befolyásolja a saját történetét. Ha más helyen lenne egy adott pillanatban mint ahol van, akkor máshova kerülne a következő időpontban. Igazak lesznek az ilyen formájú következtetések: azért van a pont most a ’3’ helyen, mert előtte a ’2’ helyen volt. Igazak lesznek az ilyen formájú tényellenes (kontrafaktuális) következtetések is: ha korábban a pont a ’11’ helyen lett volna, akkor most a ’12’ helyen lenne. A másik két esetben a véletlen dönti el a jövőt.

A fizikai determinizmusból következik a logikai determinizmus, de fordítva nem áll.

3. A „szabadság” és a „szabad akarat” kifejezések logikai grammatikája

Szabadságról és szabad akaratról többnyire emberi cselekvések és emberi döntések kapcsán beszélünk. Mondhatjuk-e, hogy egy elemi rész szabadon dönt, hogy elbomlik-e vagy sem? Nem, ez különös lenne. Önmagában egy véletlen eseményt, csak azért mert nem látható előre, nem determinisztikus, nem szokás szabadnak nevezni. Ennek ellentmond, hogy értjük, ha valaki arra hívja föl a figyelmet, hogy egy léggömb szabadon lebeg a fejünk felett. Beszélhetünk-e szabadságról állatokkal kapcsolatban? Úgy vélem igen. Teljesen értelmes a szabadon élő állatok, és a ketrecben tartott állatok megkülönböztetése. Ennnyit röviden a szavak szemantikájáról.

Vajon relációs kifejezések vagy egyargumentumú predikátumok a „szabadság” és a „szabad akarat” kifejezések? A köznyelv mindkét értelemben használja. Mondhatjuk, hogy a vádlott abban a helyzetben nem cselekedhetett, nem dönthetett szabadon, vagy nem dönthetett teljesen szabadon – ami rögtön arra is utal, hogy a szabadságnak fokozati is vannak. Máskor viszont bizonyosak vagyunk benne, hogy Júlia szabadon, azaz belsőleg vezérelve, a körülményekkel mit sem törődve választotta Rómeót. Abban semmiképp nem vagyunk biztosak, hogy mindez nem volt látható előre. Az hogy Júlia elve elrendelten, végzetszerűen választotta Rómeót, nincs ellentmondásban azzal, hogy Júlia szabadon, szabad akaratból, azaz saját érzései által vezérelve választotta Rómeót.

A szabad akarat egy érzés, amelynek első személyű ontológiája van.[6] A szabad akarat érzése maga a szabad akarat.    

4. „Fázunk és éhezünk, de szabadok vagyunk”

Mondja nekünk Petőfi Sándor a költő, és már a gyerekek is megértik sorait. Hogy lehet ez, ha a szabadság és a szabad akarat fogalma olyan nehezen érthető, annyira bonyolult, ahogyan az a filozófiai szövegeket olvasva látszik?

Bizonyos filozófiai problémák forrása a túlfeszített nyelvhasználat. Egy ilyen filozófiai kérdés, hogy létezik-e szabad akarat? A kérdés a szabadság fogalmára alapoz, csakhogy ez egy a mindennapi életben is használt fogalom, mindenki érti. A zavarok csökkentése érdekében különböztessük meg a szó köznapi jelentését: „szabad_k”, és a filozófiai használatát: „szabad_f”. Köznapi kérdésként föltéve a kérdést, hogy Júlia szabad_k akaratából fogadta-e el Rómeó közeledését, a válasz nyilvánvalóan igen. Mindenki érti, hogy ebben az összefüggésben mit értünk szabad_k akarat alatt, annak ellenére, hogy nem tudjuk megadni a ’szabad_f akarat’ fogalom szabatos, filozófiai meghatározását.

Ezek után vegyük szemügyre az örömteli eseményt, amikor a gyermek túszok kiszabadulnak a terroristák fogságából. A kiszabadult gyerekek amint meglátják szüleiket, az ölelő karjaikba rohannak. És akkor megszólal a mellettünk álló filozófus kolléga: „Látod, ez az esemény nem volt szabad_f, mert előre látható volt, hogy mi fog történni. Ugyanis az a cselekedet amelyik előre kiszámítható, az nem szabad_f. Szabad_f csak az a cselekedet lehet, amelyik nem eldöntött előre.” Sok filozófus ezen az alapon gondolja azt, hogy a szabad_f akarat, vagy a szabadság_f, és a determinizmus összeegyeztethetetlen.

A világ bizonyos szabályszerűségeket követve működik. Az un. determinisztikus törvényszerűségek azok a szabályok, amelyek az események egy bizonyos körén belül jó közelítéssel, és nagy valószínűséggel előre láthatóvá teszik, hogy mi fog történni. Ha pl. elengedek egy kavicsot, az g nehézségi gyorsulással a föld felszíne felé esik, és pályáját előre leírhatjuk az ½ x g x t² formulával. Nem minden esemény ilyen. Fény részecskéket, fotonokat sugárzunk egy félig áteresztő tükörre. A fotonok egy része visszaverődik, egy másik része megtörve pályáját áthalad az üvegen. De meghatározhatatlan, hogy melyik részecske verődik vissza, és melyik nem. Nincsen olyan természeti törvény, amelyik ezt előírná, ez az esemény véletlen. (A fényvisszaverődés, mint tömegjelenség, már nem véletlen.) És itt érhető tetten a félrevezető nyelvhasználat. A természeti törvények, mint tilalmak, tiltások is megfogalmazhatóak, pl. nem lehet a vízen járni. Ha ez mégis sikerülne valakinek, az egy természeti törvény megsértését, azaz egy csodát jelentene. Ezért gondolja sok filozófus, hogy a természeti törvények épp úgy tilalmak, vagy épp úgy előírások, mint az emberi világ tilalmai vagy parancsai. Ha az elme működése determinisztikus folyamatok eredménye, akkor az elme működését előírják a fizika törvényei, és ha ez így van, akkor az elme működése nem szabad_f.          

Nincsen gond a szabadság fogalmával, ameddig a forrása környékén, a köznapi nyelvben használjuk. A gondok akkor kezdődnek, amikor filozófiai értelmet akarunk adni a fogalomnak, az un. „szabad_f akarat” fogalmának.

Korábban említettem, hogy a kiszabadult túszok szeretteik karjaiba rohannak. Némelyik filozófus felfogásában, ez a cselekedetük nem volt szabad, mert determinisztikus, azaz előre látható volt. Ezen filozófusok szerint, akinek a cselekedetei előre láthatóak, az nem szabad. Akkor talán arra kell következtessünk, hogy csak az őrültek cselekedetei az igazán szabadok. Meglepő következmény.

Figyeljünk föl arra, hogy a szabadság fogalma nem korlátozódik az elmével rendelkező lényekre, nem korlátozódik az emberekre. Valamennyien értjük a következő örömteli beszámolót:

­­­– Miután a madárkórházban meggyógyult a sas, a madarat gondozóik szabadon engedték. Ezt mindenki érti, és elfogadja, talán csak néhány filozófus tiltakozik: szó sincs róla, hogy a madár szabadon szállna, valójában megkötözve tartják az oksági törvények, melyek agyát, idegrendszerét vezérlik. Ha lenne egy részletes modellünk a madár agyáról, meg tudnánk jósolni előre, hogy merre száll.  Márpedig egy előrelátható esemény nem nevezhető szabadnak. – így érvel a filozófus.

Kinézek az ablakomon, és a kertben szabadon szálló madarakat látok. Szoktuk etetni őket, de nem szeretnénk kalitkában, rabságban tartani egyiket sem, pedig így szabadon száz veszélynek vannak kitéve. Jót teszünk ezzel? De most jön a filozófiai probléma. Tegyük fel, hogy a madártan tudománya előre meg tudja jósolni a madarak viselkedését. Vajon ebben az esetben nincs többé értelme a szabadon élő és rabságban tartott madarak megkülönböztetésének? Helyes volna-e azt mondani, hogy egy összekötözött lábú, szárnyaszegett madár épp úgy rab a természeti törtvényszerűségek által, mint amelyik boldogan csicsereg a cseresznyefán? 

Talán tovább is mehetünk, lássunk egy másik példát.

Bizonyos mechanikai rendszerekben „szabadon futó”-nak nevezik az olyan görgőt, amelyik alkalomszerűen kapcsolatot létesít két másik görgő között, de helyzete nem rögzített, és ékszíjjal sincs semmi mással összekötve. Ez a példa azt mutatja, hogy még egy élettelen, determinisztikusan működő mechanikai rendszerben is értelmesen használható a szabadság fogalma, ellentétben azzal, ahogy egyes filozófusok gondolják.

5. Felelősség egy determinisztikus világban

Makacs tévhit még a filozófusok körében is, hogy ellenmondás van a felelősség és a determinizmus között. Mint Carnap rámutat, csak egy determinisztikus világban lehetünk felelős cselekvők. Ahol egy pisztoly magától is elsülhet, ott nem. Sokan úgy vélik, ha a tettes cselekedetét megmagyarázza nehéz gyermekkora és az őt ért későbbi sérelmek, akkor csökken, vagy végső soron meg is szűnik a felelőssége. Ez azonban tévedés. A tettes felelőssége éppen abban van, hogy a nehéz gyermekkora és az őt ért sérelmek hatására olyan módon torzult a személyisége, hogy veszélyt jelent a társadalomra. A saját személyiségéből következett a rossz cselekedet. Ha valaki kényszerítette volna a bűnös cselekedetre, akkor az mentségül szolgálna, de a nehéz gyermekkor nem személy, és ezért kategória hiba mentségnek tekinteni. (Legfeljebb enyhítő körülményként vehető figyelembe.) Ha determinisztikusnak, előre láthatónak is tekintjük a cselekedetét, akkor is ő cselekedett és nem a körülmények. Ha determinisztikusnak, előre láthatónak is tekintjük a cselekedetét, akkor is érvényes, hogy ha nem követi el, ami elkövetett, akkor nem cselekszik rosszat. A tettes büntetése nem csak a társadalom védelme végett, hanem a társadalom igazságérzete okán is szükséges, és esetleg az elzárás jó útra is térítheti.

6. Mit mond a tudomány?

Ahogy korábban többször megtörtént, most is az történik, hogy a kérdéseket a filozófia teszi föl, de a válaszokat már egy szaktudomány adja. A témának könyvtárnyi irodalma van mind a szaktudományok mind a filozófia berkeiben. Vannak érvek pro és kontra. [7] A filozófus dolga ezek után a tisztánlátás segítése, ugyanis a szaktudomány képviselői olykor meglehetősen homályosan, filozófiai pallérozottság nélkül fogalmaznak.

A Libet-kísérlet:

A Libet-kísérlet a szabad akarat és az emberi döntéshozatal természetével kapcsolatos egyik legismertebb neurofiziológiai kísérlet. Benjamin Libet amerikai neurofiziológus és csapata 1983-ban végezte el ezt a híres kísérletet, amelynek célja az volt, hogy megvizsgálja, hogyan viszonyul egymáshoz az agyban zajló idegi aktivitás és az az érzés, hogy tudatosan hozunk döntéseket. Hogy a kísérlet önmagában meggyőzően megcáfolja-e a szabad akarat_f létét, arról megoszlanak a vélemények. Számunkra kevéssé fontosak ezek a viták, mivel a szabad akarat_f létezése összeegyeztethetetlen az elme materialitsa/naturalista felfogásával, amit helyesnek tartok.[8]

Robert Sapolsky biológus, neurológus, Stanford Egyetem:

Különbség van a között, hogy te lehetsz ok-okozati mechanizmus … mi döntünk, mi okozunk dolgokat, de ez nem a szabad akarat demonstrálásának a kérdése. Valaki valahogy viselkedik, tesz dolgokat. Miért történt ez? A válasz egy része az, hogy mi történt az idegsejtekben egy tized másodperccel ez előtt, a másik része, hogy milyen ingerek érték az idegsejteket az előző percben a környezetében. És mindez összefügg a hormon szintekkel, és azzal is, hogy mi köze van ehhez az illető gyermekkorának vagy magzati életének. Mennyeire szólnak ebben bele a génjei és hogy milyen kulturális közegbe került, mert az édesanyja a kulturális közeg alapján nevelte. Ezeket együtt Sapolsky „megosztott oksági összefüggés”-nek nevezi, mint az egyén döntéseinek, cselekvésének magyarázatát.   

Sabine Hossenfelder elméleti fizikus, tudomány népszerűsítő így gondolkozik:

Nem hisz a filozófiai értelemben vett szabad akaratban. A szabad akarat ideája összeegyeztethetetlen a fizika ismert törvényeivel, és teljesen értelmetlen. A köznapi értelemben vett szabad akarat létét, amikor úgy érezzük, hogy szabadon, külső kényszerek nélkül választunk, nem tagadja. Szerinte az emergens tulajdonságok nem léteznek az alkotó elemeik szintjén. Egyetlen elektronnak nincsen vezetőképessége, értelmetlenség erről beszélni. A vezetőképesség olyan tulajdonság amelyik csak nagy elektron rendszerek esetén értelmezhető. Egyetlen oxigén atom nem gáz, ha a gázok tulajdonságait próbálnánk hozzá rendelni, akkor kategória hibát követnénk el, ahogyan ezt a filozófiában nevezik. Székek léteznek makroszkopikus szinten, de nem az elemi részek szintjén. A magasabb szinteknek azért vannak saját törvényeik, mert bonyolult kölcsönhatások tömegéből állnak. Kialakulhatnak-e olyan emergens tulajdonságok, amelyek nem következnek, nem vezethetőek le az alkotórészek tulajdonságaiból? Ezt nevezik erős emergenciának (strong emergence). Nincs bizonyíték arra, hogy a való világban ilyen jelenség előfordul. Bár van néhány matematikai példa erre. Ha végtelen számú összetevővel vagy végtelen számú tulajdonsággal rendelkezünk, akkor kaphatunk olyan rendszert, ahol az egész rendszernek lesznek olyan tulajdonságai, amelyek erős emergenciának tekinthetőek. Ezek azonban a matematika világában létező összefüggések, melyek a véges bonyolultságú fizikai világban nem fordulnak elő. A való világban semmi sem végtelen. Minket élőlényeket, a determinisztikus és valószínűségi törvények keveréke vezérel. John Conway és Simon Kochen 2006-ban matematikailag bebizonyította, hogy ha az embereknek szabad akarata van, akkor az elektronnak is van szabad akarata. Ebből azonban konrapozicióval az következik, hogy ha az elektronnak nincsen szabad akarata, akkor az emberi lényeknek sincsen. Hossenfelder megemlíti, hogy a filozófusok többsége (60%) kompatibilista, a szabad akaratban hívő libertariánusok kisebbségben vannak a PhilPapers 2020-as felmérése szerint. (Ez persze nem érv.)

7. Konklúzió

Mindezek alapján úgy tűnik, megalapozottan következtethetünk arra, hogy ellentétben a libertariánius filozófusok tanításával, nincs ellentmondás a determinizmus, az okság és a szabadság_k, szabad_k akarat, valamint a felelősség fogalmai között. De a szabad akarat_f tagadásának önmagára való kiterjesztése paradoxonhoz vezet, ezért kerülendő. Neked, kedves olvasó, aki olvasol engem, nincsen szabad akaratod a szó filozófiai értelmében, mert anyagi rendszer vagy, elméd puszta terméke az agyműködésednek. De nekem, aki hozzád szólok, szabad elmém van, melyet a saját gondolatai vezérelnek. (Természetesen ezt te is mondhatod rólam.)  Ha a kompatibilizmus fizikalista álláspontja a szabad akaratról önmagára vonatkozik, akkor ez az álláspont eliminálja az igazság fogalmát azzal, hogy redukálja az elmét a fizikai működésre. Ezzel a redukcióval önmaga igazságát is megsemmisíti. Mondom, amit mondok, és hiszem, mit hiszek, mert ez következik az agyműködésemből, ez következik egy nagyon bonyolult fizikai rendszer működéséből, de semmi sem garantálja, hogy ez a hitem igaz. Nincsen evolúciós előnye a helyes filozófiának. Paradox helyzetbe kerültünk: ha igazam van az elme materialista felfogásában, akkor nincs igazság, csak fizikai működés van. Be kell lássuk, az agyműködéstől független elme, és a filozófiai értelemben vett szabad akarat, egy szükséges munkahipotézis, melynek logikai okai vannak, és nem metafizikai. Olyan hasznos feltevés ez, mint a számok létében való hit a matematikában. Hamis, de hasznos mítosz.

Innen letölthető.

Olvasnivaló

• Ayer, Alfred Jules (1954/2004) Szabadság és szükségszerűség, in: Modern metafizikai tanulmányok, Budapest, ELTE Eötvös Kiadó.
• Bernáth László (2023) Létezik-e szabad akarat? Budapest, Kalligram, Bp. 248 oldal.
• Chisholm, Roderick M. (1964/2004) Az emberi szabadság és az én, in: Modern metafizikai tanulmányok.
• Szabó László (2004) A nyitott jövő problémája, Budapest, Typotex Kiadó.
• Huoranszki Ferenc (2001) Modern metafizika, Osiris Kiadó, a neten is megtalálható.
• Inwagen, Peter van (1975/2004) A szabad akarat és a determinizmus összeegyeztethetetlensége, in: Modern metafizikai tanulmányok.
• Ostrowick, John Montague (2006) Whether we have Free-will, and wheter it matters, doktori disszertáció, Faculty of Humanities, University of the Witwatersrand, Johannesburg. Letölthető a netről.
• Sapolsky, Robert M. (2024) Determined - The Science of Life Without Free Will, Random House UK Ltd. 528 oldal.

A témához kapcsolódó Youtube videók:

• Carnap, Rudolf (1962) Minnesotában részt vett a „The nature of causality and probability” c. konferencián, ott beszélt a szabad akaratról, Philosophy Overdose: https://youtu.be/medR504eh8Q?si=hsUGraKkUhCnHcQ0
• Hossenfelder, Sabine: I don't believe in free will. This is why. https://youtu.be/TI5FMj5D9zU?si=TcJvhOCI8TZ3Dqg5
• Hossenfelder, Sabine: You don’t have free will, but don’t worry https://youtu.be/zpU_e3jh_FY?si=IfdwSeVunzYpNwan
• Sapolsky, Robert: You have no free will at all https://youtu.be/ke8oFS8-fBk?si=buhaoSK6zo1YsoM8
• Sapolsky, Robert and Neil deGrasse Tyson: Do we have free will? https://youtu.be/pFg1ysJ1oUs?si=dN-Cd1GcaUqm-sJ3
• Determined: Life without Free Will with Robert Sapolsky https://www.youtube.com/watch?v=rv38taDUpwQ
• Doyle, Stuart: https://quillette.com/2023/11/06/robert-sapolsky-is-wrong/
• The Surgery That Proved There Is No Free Will https://youtu.be/_TYuTid9a6k?si=SYM1iaTqvtBiOpGB

Lábjegyzetek:

[1] 16. poszt: A térré vált idő, 2017.08.14.

https://filozofiaiszeljegyzetek.blog.hu/2017/08/14/a_terre_valt_ido

18. poszt: A logikai determinizmusról I. rész, 2017.08.27.

https://filozofiaiszeljegyzetek.blog.hu/2017/08/27/ahogy_lesz_ugy_lesz_639

19. poszt: A logikai determinizmusról II. rész, 2017.09.06.

https://filozofiaiszeljegyzetek.blog.hu/2017/09/06/a_logikai_determinizmusrol_ii_resz

20. poszt: Otthon maradhatott-e Caesar ama végzetes napon? 2017. 09.14.

https://filozofiaiszeljegyzetek.blog.hu/2017/09/14/otthon_maradhatott-e_caesar_ama_vegzetes_napon

62. poszt: A létezés dimenziói, 2020.04.13.

https://filozofiaiszeljegyzetek.blog.hu/2020/04/13/a_letezes_dimenzioi_207

65. poszt: Az okság metafizikájáról, 2020.06.11.

https://filozofiaiszeljegyzetek.blog.hu/2020/06/11/az_oksag_metafizikajarol

[2] A kompatibilizmus álláspontját valló filozófusok szerint a szabad akarat és a determinizmus összeegyeztethető egymással. Ez az irányzat úgy véli, hogy az emberek szabadon dönthetnek, még akkor is, ha a világ determinisztikus törvények szerint működik. A teljesség igénye nélkül: David Hume, Thomas Hobbes – Hobbes úgy vélte, hogy a szabadság az akadályok hiányát jelenti, nem pedig a determinizmus hiányát. Szerinte szabadok vagyunk, amikor cselekedeteink összhangban vannak akaratunkkal; John Locke – Locke nem azonosította magát a kompatibilizmus híveként, érvei, például a "szabad akarat illúziójával" kapcsolatos gondolatai hatással voltak a kompatibilista gondolkodás fejlődésére; John Stuart Mill – Mill a szabadságot és a determinizmust úgy próbálta összekapcsolni, hogy a társadalmi szabadság fontosságát hangsúlyozta, amely lehetővé teszi az egyének autonóm döntéseit, még egy okságilag meghatározott világban is; P. F. Strawson, Harry Frankfurt, Moritz Schlick (lásd a Die Probleme der Ethik c. művét), Rudolf Carnap, Daniel Dennett – Denett a modern kompatibilizmus egyik legismertebb képviselője. Úgy érvel, hogy a szabad akarat nem egy metafizikai képesség, hanem egy praktikus koncepció, amely lehetővé teszi az emberek számára, hogy felelősséget vállaljanak cselekedeteikért.

A kompatibilisták álláspontja az, hogy a szabad akarat gyakorlati fogalom, amely a mindennapi tapasztalatokkal összhangban működik, még egy determinisztikus világban is. E filozófusok mindegyike más megközelítéssel, de azonos céllal vizsgálta, hogyan lehet összeegyeztetni a szabadságot és a determinizmust.

[3] Quine megemlíti Doris Day dalát az írásában. „A dolgok és helyük az elméletekben” in Willard Van Orman Quine (2002) A ​tapasztalattól a tudományig, Osiris Kiadó, Budapest.

[4] Bertrand Russell (1976) Tudás ismeretség révén és tudás leírás révén, in. Miszticizmus és logika (ford. Márkus György), Magyar Helikon, p.329. Eredeti megjelenés: Knowledge by Acquaintance and Knowledge by Description (1910 - 1911), Proceedings of the Aristotelian Society, New Series, Vol. 11, pp. 108- 128

[5] Neven és mondaton véges ábc-vel, véges sok képzési szabállyal meghatározott nyelvek kifejezéseit értem.

[6] Az első személyű és a harmadik személyű ontológia megkülönböztetésével kapcsolatban, lásd John R. Searle (2000) Elme, nyelv és társdalom. A való világ filozófiája, Budapest, Vince Kiadó.

[7] Boldogkői Zsolt írása:

https://index.hu/tudomany/2013/04/06/letezik-e_szabad_akarat/

Kazai Anita írása:

https://medicalonline.hu/tudomany/cikk/egyenlok_vagyunk_szabad_akarat_tekinteteben

 [8] Bernáth László részletesen foglalkozik könyvében a Libet kísérlettel, és sok vonatkozó irodalmat is megad.