Használjunk modellt!

A korábban azzal a kérdéssel foglalkoztam, hogy nyitott-e a jövő, előre meghatározott-e a sorsunk? A kérdés a valóságos emberi életre vonatkoztatva túlságosan bonyolult, elfedi a lényeget. Egyszerűsítsük le a problémát a lényeg megtartásával, hogy jobban lássuk a logikai-filozófiai összefüggéseket. Ehhez használjunk egy filozófiai világ modellt, amelyik csak a probléma lényegére fókuszál. Több ilyen modellt, példát is bemutatok. Előtte azonban elmagyarázok három fogalmat, melyek nélkül a későbbiek érthetetlenek. Milyen lenne egy kaotikus, vagy ellenkezőleg egy determinisztikus, avagy a kettő közötti valószínűségi – azaz részben determinisztikus -- világ?

A determinizmusnak kettőse jelentése van, melyet gyakran nem különböztetnek meg, mert gyakorlatban a megkülönböztetésnek nincsen jelentősége. Az első szempont, hogy a rendszer valamely paramétere (állapota) amikor létrejön, akkor egyértelműen, pontosan meghatározott-e, vagy sem. Most csak a meghatározott esettel fogunk foglalkozni. A második szempont a rendszer jövőbeli állapota meghatározásának a korlátja, annak mértéke, ami jellemzi egy rendszer determinisztikus mivoltát. Bemutatom ezeket négy, csak a filozófiai lényegre összpontosító példán.

(i) Útkereszteződés

Forgalmas útkereszteződésben állunk, hömpölyög az autók áradata. Minden rendben van, az autók hol az egyik, hol a másik irányban haladnak. A járművek haladása rendezett sorokban történik, előrelátható, hogy mikor áll meg az egyik irány és mikor indul a másik. A forgalomirányítás modelljében gondolkozva rend van a kereszteződésben. Most hirtelen elromlanak a közlekedési lámpák. Néhány autó bennragad a kereszteződésben, mások össze vissza hajtanak. A becsatlakozó utcákon néhány perc alatt torlódás jön létre, zűrzavar keletkezik. Megszűnt a rend a közlekedési szabályok nézőpontjából -- egy adott modellből nézve -- de a járművek fizikájának a szintjén, fizikai modellel szemlélve az eseményeket megmaradt a szabályszerű viselkedés. Mindkét esetben biztosak vagyunk benne, hogy az autók mozgása megmagyarázható. Mindkét esetben hiszünk abban, hogy a járművek mozgásának mindig volt oka, és ezekben az okokban pedig azért hiszünk, mert úgy véljük a kaotikus esetben is szabályoknak megfelelően történik minden, csak ezeket az egyedi szabályokat nem szervezi egységbe a jelzőlámpák működése. Nem változtak meg a fizika törvényei, és a motorok, kerekek, fékek és lámpák viselkedése továbbra sem mond ellent a fizika törvényeinek. A vezetők is tudják merre akarnak menni, és ilyen módon minden mozgás -- a zavaros is -- megmagyarázható, csak ez a magyarázat jóval bonyolultabb a második esetben, mint az elsőben, amikor még jól működtek a jelzőlámpák. Ez a példa érzékletesen mutatja, hogy egy jelenség bonyolult, emberi szempontból szabálytalan mivolta önmagában nem alapozza meg azt, hogy nincsenek a mélyében érvényben olyan másfajta szabályszerűségek, amelyek magyarázatul szolgálnak arra ami történik. A szabályszerűségek és okok megtalálása attól függ, hogy milyen modellel kívánjuk megmagyarázni az eseményeket. A választott keret elmélettől függ, hogy van-e szabályszerűség és mi az ok. E közlekedésről szóló példa ugyan szemléletes, mert a mindennapi életből vett ismert jelenség, de nem elég elvont, és túlságosan összetett, sok részletkérdés vonja el a lényegről a figyelmünket. Nem tudjuk egyszerű matematikai eszközökkel leírni ami történik, így filozófiai vizsgálódás céljára kevésbé tanulságos. Lássunk egy jobb példát.

(ii) Háromszög

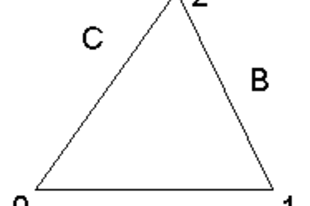
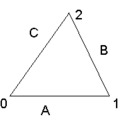
Képzeljünk el egy egyenlő oldalú háromszöget melynek minden oldala egységnyi hosszúságú, és három oldalának nevei: A,B,C (3. ábra). Ekkor a háromszög kerületének minden egyes pontját egyértelműen meghatározhatjuk úgy, hogy A és C találkozási pontjából kiindulva B irányába kijelölünk egy haladási irányt, így minden oldalnak lesz eleje és vége. Az oldalak elejéhez 0, a végükhöz 1 számot rendelünk, és a közbenső helyeket is arányosan értelmezzük. (Nem mondom, hogy elnevezzük, mert nincs annyi név ahány valós szám van. ) Az A-hoz tartozó számokhoz nullát, a B-hez tartozó számokhoz 1-et, míg a C-hez tartozó számokhoz 2-t adunk hozzá. A háromszög kerületének összes pontja így a nulla és három tartományba fog esni. Legyen három ilyen háromszögünk, és mindegyikben pattogjon egy pont vagy parányi kör vég nélkül. Diszkrét időskálán képzeljük el a pont mozgását, és csak arra figyelünk, csak azt értelmezzük, amikor a pont a háromszög egyik oldalán van. Azzal nem foglalkozunk, hogy miképp és mennyi idő alatt ér oda a pont. Föltételezzük, hogy minden esetben egy diszkrét időegységnyi idő alatt érkezik a következő helyre a pont. Ezek pályáját a háromszögekben három különféle szabály határozza meg.

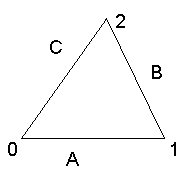
(0) Mindhárom esetben a pont minden diszkrét időpontban egy és csak egy teljesen pontosan meghatározott helyen van. Ez a kikötés csak a mi modellünkre érvényes, amelyik idealizálja a valóságos történéseket. A valóságban sok esetben nem tudjuk teljes pontossággal meghatározni egy rendszer paramétereit, sokszor közelítéssel élünk, vagy valószínűségi eloszlás függvényt rendelünk némelyik rendszer jellemzőhöz. Hogy ez a bizonytalanság objektív tény-e, avagy a mérési bizonytalanságból fakad, az más kérdés, és sokszor nem eldönthető.

(1) Az első háromszögben, ha a pont valahol van, akkor a következő oldalba való becsapódás helye egyforma valószínűséggel bármelyik pontja lehet a háromszög oldalának, még az is előfordulhat, hogy egyhelyben marad a pont.

(2) A második háromszögben a pont valamelyik oldalba való becsapódási szöge megegyezik a visszaverődés szögével.

(3) A harmadik eset a másodikhoz hasonlít azzal az eltéréssel, hogy a visszaverődési szög nincs pontosan meghatározva, csak annyi biztos, hogy a visszaverődő pont iránya két szélső érték közé esik, de hogy melyik lesz a két szélső érték között a tényleges visszaverődés szöge, arra nincs szabály, az véletlenül következik be.

Ezeket mutatják az alábbi ábrák (4. ábra). Érdemes lenne azt is megvizsgálni, miképp változna a modell, ha több, esetleg nagyon sok parányi kör pattogna a háromszögekben, és azok a háromszögen belül egymással is ütközhetnének, esetleg vonzanák, vagy taszítanák egymást, vagy másképp hatnának egymásra.

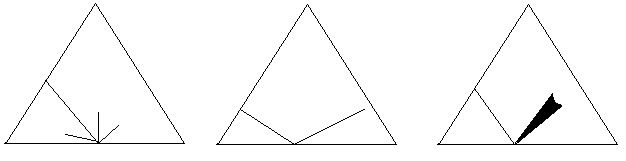
A pontok minden egyes oldalba való becsapódásához tartozik egy egyértelmű szám. Így az előző feladat egy pont pattogása esetén átalakítható számsorozatok meghatározásává. A második esetben ezt a számsorozatot egyértelműen meghatározza a becsapódási és visszaverődési szög egyenlősége, viszont az első és harmadik esetben véletlen sorozatot kapunk. Véletlen sorozaton a következőt értem: olyan feltételezett végtelen sorozat részsorozata, amelyik semmilyen determinisztikus automatával (pl. Turing géppel) nem generálható. A determinisztikus kikötés ebben a meghatározásban nem lényeges, hiszen két végtelen véletlen sorozat egybeesése kizárható. Viszont lényeges annak a belátása, hogy bármilyen véges n tagú számsorozathoz konstruálható olyan matematikai formula vagy véges automata, amelyik első n tagja pontosan az adott sorozat. Ebből következik, hogy ha csak véges sok szám áll a rendelkezésünkre, abból teljes bizonyossággal nem tudjuk kikövetkeztetni, hogy a sorozat véletlen-e, vagy ellenkezőleg valamilyen szabály vagy automata hozta létre. Így annak a filozófia érvnek, hogy véges sok megfigyeléssel nem tudjuk bebizonyítani valamely végtelen sok esetre értelmezett törtvényszerűség létét, a megfordítása is igaz, véges sok megfigyeléssel önmagában az sem cáfolható, hogy a háttérben meghúzódik valamilyen bonyolult szabály.

Matematikai nézőpontból másodlagos, hogy a pattogó pont egy kör kerületén, vagy egy háromszög oldalain, vagy egy egyenesen helyezkedik el. A lényeges az, hogy a pont egy véges szakaszt ciklikusan bejár ahol az i+1-ik diszkrét időpontban elfoglalt helyét az i-ik időpontban lévő helye határozza meg valamilyen függvény által. Sejtésem szerint, feltéve, hogy a szakasz folytonos, és a pont egymás után irracionális számoknak megfelelő pozícióba kerül, a pont végtelen idő alatt egyenletesen kitölti a szakasz helyeit, ha viszont a pont helye racionális számok sorozatának felel meg, akkor a pont ciklikusan ismétlődő pályán halad. E két állítás tartalmazza az időt, de igazsága időtlen. (De bizonyítással sajnos nem tudok szolgálni.) Mindkét esetben feltételeztük, hogy a pont bármely helyzetéhez tartozó következő helye egy függvény által egyértelműen meghatározott. Másként mondva a pont pályája determinisztikus ebben a két esetben. Ne gondoljuk azonban, hogy ennek a determinizmusnak a jellege egyszerű. Vajon miféle képességek, milyen eszközök kellenének ahhoz, hogy a pont helyét bármely későbbi időpontban előre lássuk?

Vizsgáljuk először csak a determinisztikus eseteket, amikor a pont bármely két egymás utáni helye egyértelműen meghatározza a következő helyét. Első lépésben tegyük fel, hogy csak egy pont mozog ciklikusan a véges szakaszon. Ha a pont helyei racionális számoknak felelnek meg, melyek tört formában ábrázolhatók, akkor egy végtelen képességű matematikus bármely későbbi időpontban meg tudja határozni a pont helyét formulákkal való számolással, viszont egy digitális számítógép amelyik numerikus számításokat végez, már racionális számokkal is kis hibával számol, erre nem képes. Azért nem, mert nem törtek, hanem számsorozatok alakjában ábrázolja a számokat. Pl. az ’1/7’ számnak egy végtelen számsorozat felel meg, aminek csak töredékét képes a számítógép ábrázolni (pl. 1/7≅0.142857143). A gép akkor is csak rövid távon képes jó közelítéssel meghatározni a pont helyét, ha az irracionális számok sorozatán halad. Ám ekkor már a korábban említett végtelen képességű matematikusnak is számok aktuális végtelen sorozataival kéne tökéletesen pontosan számolnia, ami csak úgy lehetséges, hogy ezekre a számokra formulákon belül egy-egy számjellel (pl. π) hivatkozik. Viszont egy ideális analóg automata képes lenne pontosan meghatározni a pont helyét bármely későbbi állapotban, csakhogy ideális analóg automata a fizikai valóságban nem létezik.

A második esetben vegyük azt a még mindig determinisztikus verziót, amikor nagyok sok egymással is ütköző kicsiny kör pattog. Az ütközések következményeit is egy determinisztikus szabály rögzíti. Analóg automatával ekkor is célt érhetünk, de a végtelen képességű matematikus valószínűleg elvileg megoldhatatlan problémák tömege elé kerül, és a legkevesebbre a számítógépek képesek. 

Részben determinisztikus viselkedést feltételezve csak rövidtávon, és csak adott hibával tudjuk megjósolni a pattogó pont, vagy körök helyét. Ekkor nem fontos mi modellez – véges automata, Turing gép vagy analóg számítógép –  előre látási lehetőségek vannak, de korlátozottak.

Miképp változna a modell ha háromszög helyett gömböt választanánk, és az objektumok nem két dimenzióban, hanem háromban (vagy többen) mozognának, és a gömb tágulna? Ezen kérdések megválaszolása komplikált matematikai apparátust igényel, én most inkább tovább egyszerűsítem a modelleket.

(iii) Egydimenziós világ

Még egyszerűbbé válik a példa, és könnyebben modellálható a filozófiai tartalom lényegének megőrzése mellett, ha a pont mindössze egy véges egyenes szakaszon halad. Annyival is legyen egyszerűbb a vizsgálódás, hogy a szakasz csak diszkrét helyekből, adott esetben 32 helyből álljon, 32 egymást követő természetes szám növekvő elrendezése szerint. Háromféle szabály alapján három véges világot képzelünk el. Mindhárom véges világ 32 helyből áll, az idő is diszkrét, és egyetlen dolog van mindhárom világban, és az az egy dolog időnkét változtatja a helyét. A szabályok felírhatók formális nyelven, rekurzív függvény formájában. Fontosak ezek a formulák, a később visszatérek rájuk. Ezekben az egyszerű világokban lévő dolgoknak a helyük az egyetlen jellemzőjük. A modelleknek diszkrét belső idejük van, amelyik folyamatosan, egyenletesen előre múlik és körbe jár.

A példák lefordíthatók véges automata modellek nyelvére is – két esetben ezek nem determinisztikus automaták -- aminek egy konkrét működő példája az Internetről való letöltés után ki is próbálható. A táblázatkezelő modellek mutatják a modell világában lévő objektum helyét és idejét.

http://ferenc.andrasek.hu/modellek/det-hu.xlsx

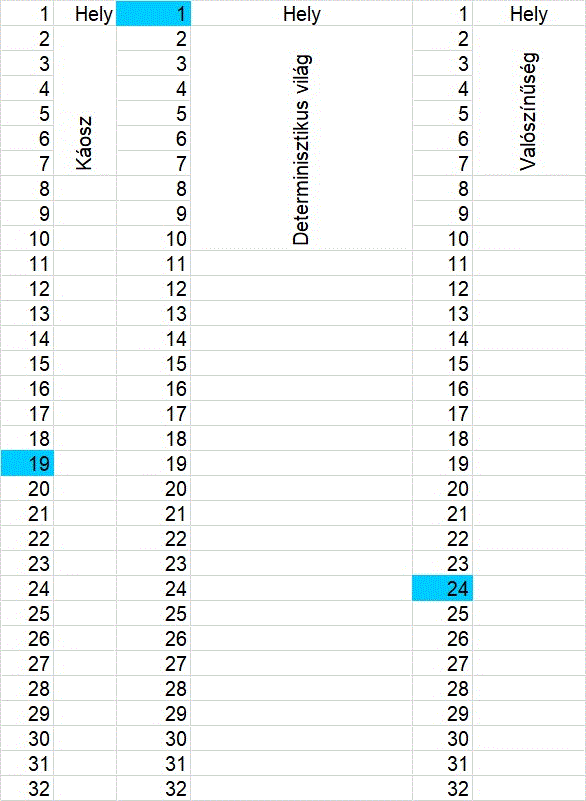
5. ábra

 A táblázatkezelő modell három példát mutat be. A három példa szemléletesen mutat három világot: egy teljesen kaotikusat, egy teljesen determinisztikusat, és egy részben determinisztikusat (valószínűségit). A második és harmadik világban érvényesek szükségszerű igazságok: pl. a pont soha nem megy hátra, és véges idő alatt eléri a végső helyzetét. Bizonyos szükségszerű állítás még az első, kaotikus világban is igaz: a pontnak minden időpontban van egy és csak egy helye, de a pont történetéről már semmiféle biztos előrelátással nem élhetünk. (Egy más bonyolultabb modellben, ahol a pont helye csak valószínűségi függvénnyel adott, a helyek statisztikai eloszlás függvény formáját öltik.) Nem tudjuk megadni minden esetben, hogy mi fog történni, de bizonyos hogy le fogja írni a pont haladását egy függvény. Ennél több is igaz. Meghatározható azon függvények véges halmaza amely elemei között ott lesz a jövőt leíró függvény is. Ez a függvény pontosan leírja a jövendőt, de nem határozza meg azt. Annak köszönhetően, hogy ezek véges világok, mindhárom esetben ki is számolható az összes lehetséges függvény. A pont véges idő alatti világtörténete 32 diszkrét időpontot feltételezve az alábbi szabályok szerint alakul. Ezek valójában rekurzív függvények.

(0) Mindhárom esetben a pont minden diszkrét időpontban van egy és csak egy teljesen pontosan meghatározott helyen. (Mint korábban említettem, ez a kikötés csak a mi modellünkre érvényes, amelyik idealizálja a valóságos történéseket.)

(1) Az első esetben a pont bármelyik x helyet követő állapot után bármelyik másik y, vagy éppen azonos (x=y) helyre kerülhet. Így a számok tetszőleges véletlen sorozatát kapjuk.

(2) A második esetben a pont elindul a ’1’-jelnek megfelelő helyből, a következő hely ahova érkezik a ’2’ jel, majd a ’3’ jelhez jut, és így tovább egészen addig amíg az utolsó, a ’32’ jel által jelölt helyig elér. Ez után ismét a ’1’ helytől folyatatja tovább az útját. A szabály részben formalizált, ’A sorozat’ szemléletű nyelven.

Ha időpont<32 Akkor következő-hely=jelenlegi-hely+1; más esetben következő-hely=1.

(3) A harmadik esetben a pont soha nem megy hátra, de nem megy előre többet, mint három egység. Mehet előre egy, kettő, három távolságegységet, vagy éppen semmit. Hogy pontosan mennyit megy előre az a véletlenen múlik. A szabály részben formalizált, ’A sorozat szemléletű’ nyelven:

Ha időpont<32  Akkor (következő-hely=előző-hely + véletlen szám, kivéve ha a hely túlmutatna a határon. Utóbbi esetben levonunk a helyből 32-t); más esetben a következő-hely=1.

A fenti (2) és (3) formulákban szereplő ’időpont, jelenlegi-hely, következő-hely’ kifejezések egy csak a kibertérben, a számítógép működése közben értelmezett program nyelv változói, melyek tényleges értéket működés közben kapnak. Ezek nem logikai-matematikai formulák a szó szigorúan pontos filozófiai értelmében. Itt a formulákban szereplő ’idő’ változó használja a mindenkori ’jelen’ és ’múlt’ fogalmát.

Ezek után vizsgáljuk meg az alternatívák számát. Az alábbi számok a lehetséges világtörténetek számát mutatják, melyek könnyedén kiszámolhatóak, meghatározhatóak a fenti szabályok alapján:

kaotikus világ: 45,671,926,166,590,700,000,000,000,000,000,000,000,000,000,000

determinisztikus világ: 1

valószínűségi világ: 4,611,686,018,427,390,000

 A számok mutatják, hogy ezek lényegesen különböző világok, miközben az „ahogy lesz, úgy lesz” érv, mint cáfolhatatlan igazság, mindegyikükben érvényes. Két esetben nem tudjuk vagy nem tudjuk pontosan meghatározni a jövőt, a pont történetét, de azt mégis biztosan tudjuk, hogy létezik egy függvény ami leírja a jövőt, a pont eljövendő történetét. Az előző mondatban szereplő „létezik” szó az ami a filozófiai görcsöket okozza. Létezik a jövőt leíró függvény, de nem tudjuk előre melyik az, és két esetben nem is tudhatjuk, nem tudjuk előre kiszámolni a világvonalat jelentő függvényt. Ugyanakkor a függvény semmilyen befolyással nincsen az eseményekre, csak leírja azokat. Ha rosszul írná le, akkor is minden ugyanúgy történne, mert a modell belső törvényszerűségei határozzák meg a jövőbeli eseményeket és nem a világvonalak. Konstruálható olyan modell is, ahol a világvonalak oksági hatással bírnak, mert előírják az eseményeket, de ez a modell nem ilyen. És van értelme az előreláthatatlanság és előreláthatóság értelmezésének és fokozatbeli megkülönböztetésének a második és harmadik példa alapján. Más pontosságú előrelátásokat tesz lehetővé a második, és mást a harmadik világ, és ebből következően mások a bennük érvényes természeti törvényeket megfogalmazó állítások is.

(iv) Pénzfeldobás

Képzeld el, hogy a világ egyetlen pénzérméből áll, annak is csak két állapota lehet, fej vagy írás, és ez a világ összesen három pillanatig létezik. Keletkezik, van, majd eljön az utolsó pillanat. Teljesen mindegy hogy ebben a világban létezik-e valamilyen természeti törvény, ami kiszámíthatóvá teszi, vagy valószínűsíti, az érme következő állapotát, vagy sem. Az érme összes lehetséges történte ettől függetlenül meghatározott az alábbi módon:

1. fej fej fej; 2. fej fej írás; 3. fej írás fej; 4. fej írás írás; 5. írás fej fej; 6. írás fej írás; 7. írás írás fej; 8. írás írás írás

Bárhogy dobod föl háromszor a pénzérmét, a valóságos eseménysor ott lesz a fenti sorozatok között.

Vegyük azt az állítást, hogy: a második dobás fej. És ezt az állítást a második dobás előtt tesszük. Van-e igazságértéke ennek a mondatnak, már most, amikor még nem dobtuk föl másodszor az érmét? A logika szerint van – csak nem ismerjük – mivel a dobás illeszkedni fog az egyik lehetséges sorozatra, arra, amelyik a valóságos dobás sorozatot leírja. Most persze még nem tudjuk, hogy melyik az, de ott van a fennebb felsorolt lehetőségek között. Vajon a logikának ebből a feltevéséből valóban az következik, hogy akkor a pénzfeldobás nem véletlen, hanem előre kiszámítható, azaz determinisztikus esemény? Nyilván nem.

Hol a hiba a logikai determinizmusban?

Mutatok példát egy olyan világra, ahol nem törvényszerűségek (szabályok) hanem az előre rögzített világvonalak határozzák meg a jövőbeli eseményeket. Itt ezért tehát oksági kapcsolat van a tényeket leíró grafikon és a modell belső valósága között. (A való világban nincs ilyen grafikon.) A modell sokban hasonlít a korábbiakhoz, melyet röviden ismertetek.

http://ferenc.andrasek.hu/models/time-series2dim.xlsx

Ez egy determinisztikus világ -- lényeges, hogy az -- ahol az objektum világvonalát a táblázatkezelő egyik munkalapján található diagram ábrázolja. A modell egydimenziós világában egy objektum halad előre. A világvonal előírja, hogy melyik időpillanatban hol van az objektum. Az objektum a hetedik pillanatig előre halad, utána három idő atomig áll, majd előre megy a tizennegyedik helyig, ahol visszafordul, és a tizenegyedik helyen fejezi be pályáját.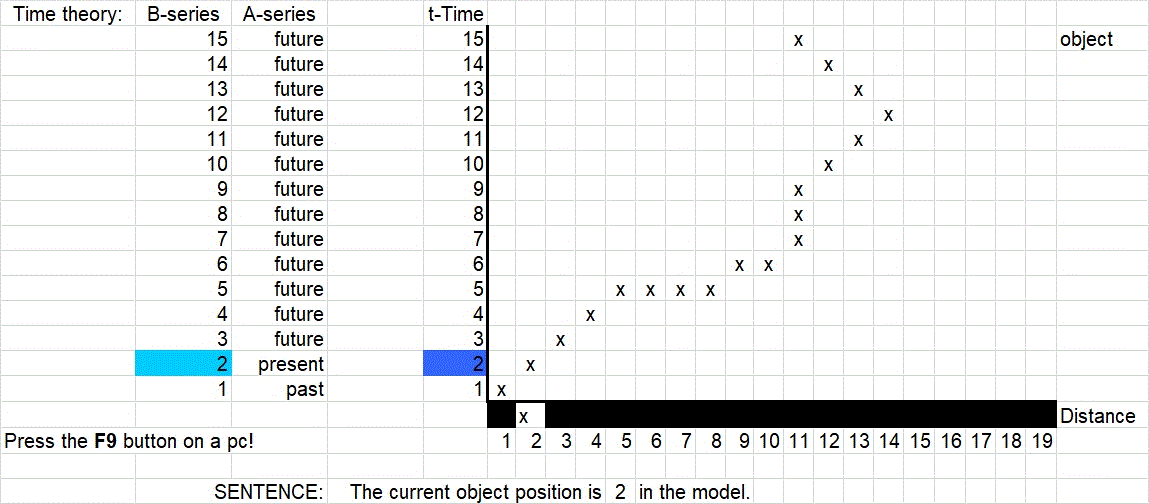6. ábra

A világvonal természetesen szabadon módosítható, de célszerű, ha most csak az időben előre haladó lehetséges világvonalakban gondolkozunk. A modell az egyik munkalapon a mindenkori jelent jeleníti meg, és itt található egy ennek megfelelő mondat is: „Az objektum most a 2-es számú helyen van.” Ez egy alkalmi mondat, nem pedig perfekt mondat, nem propozíció. A mondat annak megfelelően változik, hogy ténylegesen hol van az objektum, és a mondat mindig igaz. A másik munkalapon az igazság időtlen dimenziójában ábrázoljuk objektum világvonalát. Két idő dimenzió alkalmazásával a korábban ismertetett módon jelenítjük meg, a minden időponthoz tartozó jelent, és az objektum akkori helyét. Ezen a munkalapon perfekt mondatokat fogalmazhatunk meg az objektumra vonatkozóan.  A modell igazra vagy hamisra értékeli az állításunkat annak megfelelően, hogy a modell által előírt világvonal igazolja-e az állítást vagy sem.

7. ábra

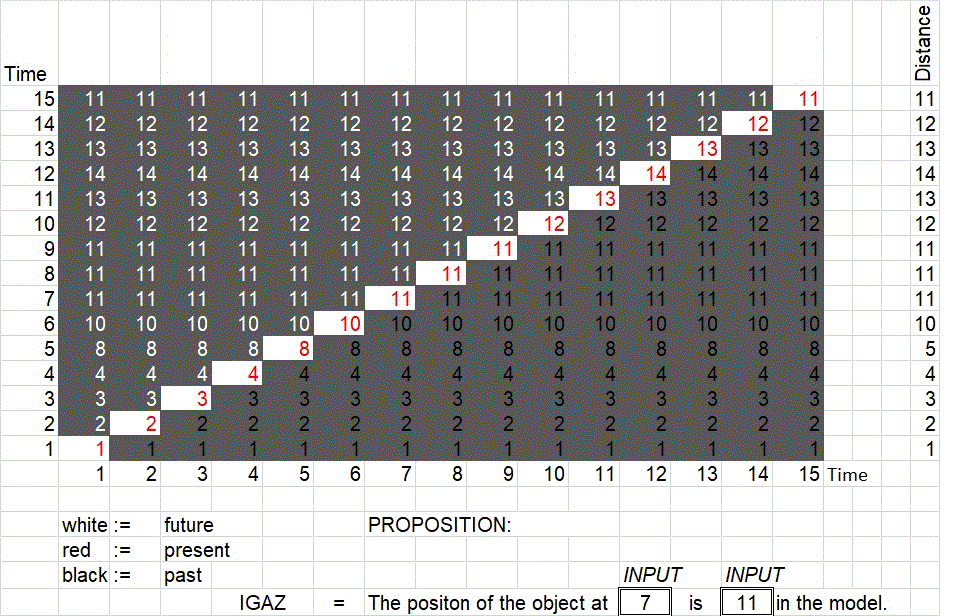
Ebben a determinisztikus modellben jól láthatóan a jövőre vonatkozó állításoknak épp úgy van igazságértéke, mint a múltra vonatkozóknak. Ez azért van így, mert ez egy determinisztikus modell, és a tér-idő grafikon nem a lehetőségeket, hanem a tényeket ábrázolja, ami az alapja az logikai értékeknek.

Ezt írtam korábban: „Adott tehát azon mondatok halmaza, melyek életed tényeit írják le, bár nem ismered ezek java részét. Ez azonban mellékes, életed jövőbeli tényei léteznek, csak ismeretlenek előtted. Életed tehát e tények által előre meghatározott. Adott tehát azon mondatok halmaza, melyek életed tényeit írják le, bár nem ismered ezek java részét. Ez azonban mellékes, életed jövőbeli tényei léteznek, csak ismeretlenek előtted. Életed tehát e tények által előre meghatározott.”

Most már belátható, hogy ez téves következtetés volt. A világ eseményeit a fizika törvényei határozzák meg. Amennyiben a fizika törvényei determinisztikusak, úgy a jövő előre meghatározott, de nem a világvonalak grafikonja által, mert az csak következmény. Ha a fizika törvényei nem determinisztikusak, akkor is létezik a korábbiakban meghatározott események (függvények) teljes halmaza, de azok pusztán lehetséges események. Ebben az esetben a jövő nyitott, mert nem meghatározott, hogy melyik valósul meg a lehetséges események közül. A modellekben meghatározott az összes lehetséges események halmaza, de csak a determinisztikus esetben tudjuk kikövetkeztetni, hogy ezek közül melyik fog megvalósulni. Nagy különbség van egy lehetséges és egy valóságos tény között. A függvények vagy a lehetséges tények halmaza csak bizonyos modellek esetén befolyásolja a történéseket. Mint korábban írtam egy példa kapcsán: „Ontológiai szakadék tátong a logikai-matematikai törvények világa és a fizikai események világa között. Az objektum történetét nem az határozza meg, hogy a jövőjét leíró függvény szükségszerűen létezik, hanem az az oksági kapcsolat, ami a modell világában lévő függvény – a x-ek egy grafikonja – és a modell valóságos időbeli működése között van. Az oksági kapcsolat, a modell mint automata determinisztikus működése nélkül, a függvény nem befolyásolná az eseményeket, nem befolyásolná a jövőt. Csak azért határozza meg a x-ek által leírt grafikon a modell eseményinek történetét, mert ez egy ilyen modell, így működik. Lehetne másmilyen is, olyan is, amelyik valószínűségi alapon működik és nem determinisztikusan. Ekkor már nem látnánk előre a jövőt a modell világán belül.”

Jövőre vonatkozó állítások

Determinisztius modell esetén kiszámíthatóak a jövőbeni események, állapotok, és azok egy diagramon ábrázolhatóak – a múltbeli események csak lineáris oksági láncok esetén következtethetőek ki. Ha tudnánk, hogy melyik függvény írja le a jövőt, mert a modell determinisztikus, a függvény akkor sem volna azonos azzal, amit leír. Ha ismernénk a jövőt leíró függvényt valamely v időpontban, amely leírja a jövőt egy későbbi w időpontban, attól az a tény, ami a jövőben fog létre jönni még nem létezik a jelentben. Akkor miért feltételezi a klasszikus kétértékű logika, hogy a jövőbeli w időpontra vonatkozó állításnak is van már most, a v időpontban igazságértéke? Két indok is van.

1. A logika egyik – ha nem a legfontosabb -- feltevése, hogy ha a premisszák igazak, és a következtetés helyes, akkor a következmény is igaz. Még akkor is igaz, ha a jövőre vonatkozik. Nehézséget okozna a klasszikus kétértékű logika elmélete számára a jövőre vonatkozó állítások kétértékűségének korlátozása, hiszen ezt nehéz lenne megadni pusztán a logikai szerkezet alapján. Ezért feltételezi a klasszikus kétértékű logika – az elmélet teljessége és egyszerűsége kedvéért – hogy minden a jövőre vonatkozó perfekt mondatnak (más felfogásban propozíciónak) is van logikai értéke, csak még hozzáférhetetlen, ismeretlen. Ez a különös feltevés kevesebb zavart okoz, mint valamilyen bonyolult alternatív rendszer kidolgozása. Ugyanakkor kidolgoztak olyan többértékű, nem klasszikus logikákat, ahol a jövőre vonatkozó állításoknak neutrális értéke van, sem nem igazak, sem nem hamisak, és vannak az idővel foglalkozó más logikai rendszerek is, amelyek túlmennek a klasszikus logikán.
2. A létezésnek a köznapi és filozófiai jelentése (értelme) eltér a formális (szimbolikus) logika gondolkozásmódjától. Quine figyelmeztet rá – a logika az egzisztenciális kvantorral fejezi ki a létezést, de az egzisztenciális kvantor által kifejezett létezés nem időben értendő. A klasszikus logikában használatos egzisztenciális kvantor egyaránt jelenti a múltat, jelent és a jövőt. Egy idő változót tartalmazó nyitott mondat terjedelme az időpontok halmazán értendő, és annak nem része a jelenhez való viszony. A klasszikus kétértékű logika szerint a jövőre vonatkozó perfekt mondatoknak van (időtlen, állandó) igazságértéke már most, a jelenben. (Mindegyiknek) Ez az elmélet belső, szakmai feltevése, amely egyfajta idealizáció, melyhez hasonlót minden egzakt tudomány alkalmaz. Egy példa jobban érthetővé teszi mindezt. Cseréljük ki az egyik perfekt mondatban az időadatot egy változóval, amelyik az időpontok tartományán értelmezett. Egy ilyen nyitott mondat: ’Pomázon fáklyás felvonulást tartanak t – időpontban’. A szimbolikus (matematikai) logika nézőpontjából, ezt a nyitott mondatot bármelyik múlt, jelen vagy jövőbeli időpont igazra értékelheti, amennyiben akkor és ott valóban fáklyás felvonulást tartanak, tartottak vagy tartani fognak. Nem szükséges, hogy az igazságot meglapozó tény már most a jelenben létezzen, elegendő, ha a jövőben fog létezni, mert a logika így, időtlen értelemben érti a létezés fogalmát az ő matematikai nyelvén. Ebben az értelemben a logika és a matematika eternalista. (Pl. a halmaz és eleme reláció is időtlen. Ha ’Szókratész bölcs’, és ezt a halmazelmélet nyelvén fogalmazzuk meg, akkor egy időtlen, örök igazsággá válik.) A köznapi nyelv vagy a program nyelvek nem így gondolkoznak, és azok a filozófusok, akik szintén a köznapi nyelvet használják téziseik magfogalmazására, szintén időbeli vonzattal használják a létezés fogalmát. Ezért számukra a logika vagy a matematikai fizika gondolkozásmódja érthetetlen. A létezés logikai, és nem filozófiai értelmű fogalma alapozza meg, hogy mindhárom esetben minden jövőre vonatkozó állításnak van egyértelmű igazságértéke, csak nem tudjuk idő előtt, hogy mi az.

Az idő B-sorozat alapú elmélete a logika és a matematikai-fizika szemlélete – az igazság lét-dimenzója -- az idő A-sorozat alapú szemlélete a mindennapi lét dimenziója látásmódja. A filozófiai probléma a kettő egymásra való reflexiója. Ezért mondja Szent Ágoston: „Mi hát az idő? Ha senki sem kérdezi, tudom; ha kérdik tőlem, s meg akarom magyarázni, nem tudom.”

Létezik-e jelen?

A ’jelen’ fogalma valami elme független tulajdonságot fejez ki, vagy csak számunkra, emberek számára létező pszichológiai fogalom? A válasz attól függ, hogy milyen keretelméletben gondolkozunk. Az idő és a létezés más fogalmát használja a matematikai-fizika és a logika, és más fogalmát a mindennapi élet, a józan ész, és a számítógépes programok. A fizikusok derítették ki a legtöbb meglepő tényt az időről. A Speciális relativitáselmélet felfogását személetesen ábrázolja a Minkowski-féle négydimenziós tér. Ebben a jelen mint a fénykúp kezdőpontja jelenik meg, amelyik mutatja, hogy mely események hathatnak a jelenre, és a jelenből kiindulva mely jövőbeli eseményekre lehetünk hatással. Az események ábrázolása ebben a koordináta rendszerben időtlen. A múlt épp úgy létezik, mint a jövő. Ez az időtlenség azonban nem a relativitáselmélet következménye, hanem a matematika alkalmazásáé. Egyszerűbb példán is jól látható ez. Az az ábra (2. ábra) is matematikai-geometriai szemlélettel ábrázolja a történéseket, és az események azon a grafikonon is időtlenül jelennek meg a mindennapi lét nézőpontjából, amelyikkel korábban Caesar életét ábrázoltam. A múlt eseményit ábrázolja a grafikon, miközben a grafikon maga a szemlélője számára a jelenben van. A newtoni fizikában is így jelenik meg a valóság. A mozgás ábrázolása mint az út-idő függvény deriváltja, maga nem mozog, hanem csak egyszerűen van, létezik.  A mozgást leíró függvény grafikonja maga nem mozog, hanem statikus. A statikus szöveg világában nem is lehet más, szükségszerűen olyan amilyen.

A logika nézőpontjából a múlt, jelen és jövő relációként ábrázolható ellentmondásmentesen. [i] Az idő kérlelhetetlen múlása az időskála szigorú rendezésében jelenik meg: ha két időpont nem azonos, akkor nem is lehet egyidejű. Egy következő időpont nem lehet egyidejű a mostanival, nem lehet ugyanaz az idő. (Csak diszkrét időskála esetén kezdődhetne határozott névelővel az előző mondat.) Ugyanez az események osztályára nem igaz, az események osztálya parciális rendezést alkot egy időskálára vonatkoztatva, ahol az időskála segítségével címkézzük föl az eseményeket. A ’jelen’ fogalmából ez jelenik meg az igazság lét-dimenziójában. A ’jelen’ fogalma, ahogy számos filozófus vagy költő a hétköznapi nyelv jelentésével kifejezi, a matematikai logika nyelvén kifejezhetetlen az igazság dimenziójában (a statikus szövegek világában), ezért nem része a fizikának. Mindazonáltal a filozófusok által kutatott rejtélyes mindenkori ’jelen’ része az objektív (elme független) valóságnak, bár csak a kibertérben (vagy a filmen) jeleníthető meg.

Lehetetlen olyan klasszikus kétértékű formális (matematikai) logikát csinálni, ahol a mondatoknak változó igazságértéke van a jelen függvényében, viszont a számítógépek program nyelvei épp ellenkezőleg, mindig a jelenben gondolkoznak. Láthattuk a korábbi nagyon egyszerű táblázatkezelő modelleken, hogy a valóságos időben és események hatására kapnak értéket az egyes program változók, és a formulák értéke annak megfelelően változik, azaz nem statikus. Ez alapvető eltérés a filozófiai logika szemléletéhez képest. A kettő összekeverése viszont zavart okoz. Az un. változó igazságértékű propozíció, amiről többen írtak, valójában egy nyitott mondat, semmi szükség a feltételezésére. Sok filozófus ezt nem érti. Pl. Dean W. Zimmerman egyhelyütt a következő A-sorozat jellegű definíciót adja[ii]:

p-is True at T =df It was, is or will be the case that: p is True and T is present illetve: x is F at T =df x is F and T is present

Vajon szerinte az utóbbi miben különbözik ettől a hagyományos formulától: F(x,t) =df F(x,t) & t-present? Adjunk értékeket a változóknak és egyben interpretáljuk is azokat, hogy értsük, mit mond ez a definíció: 

Esik az eső (Pomázon, 2017. szeptember 2-án) =df  Esik az eső (Pomázon, 2017. szeptember 2-án) & most 2017. szeptember 2-a van.

Vajon mire gondolt a szerző? Úgy tűnik, mintha szerinte csak a jelenben állíthatnánk egy tényt a pomázi időjárásról, ami abszurdum. Ha viszont az ’F(x,t)’ formulát a kibertérben használjuk, ahol az automata ad értéket a mindenkori jelenben a változóknak, akkor pontosan azt az értelmet kapjuk meg, amire Zimmerman és az idő A teoretikusai gondolnak.

Az utóbbi két bejegyzés szövege letölthető innen:

http://ferenc.andrasek.hu/pdf-papers/time/logikai-determinizmus7.pdf

[i] v.ö. Matt Farr: On A- and B-Theoretic Elements of Branching Spacetimes, Synthese September 2012, Volume 188, Issue 1, pp 85–116 Szerinte a reláció argumentumába időpont helyett időskálát helyezve vagyunk képesek kifejezni az A sorozat természetét, és ez több, mint az általa „perspektivizmusnak” nevezett relációs felfogás.

[ii] The A-Theory of Time, The B-Theory of Time, and ‘Taking Tense Seriously’ in Dialectica, Vol. 59, N° 4 (2005), pp. 401–457 Dean W. Zimmerman