Andrés Gallois változással kapcsolatos gondolatiról írt 54. posztomat újra olvasva észrevettem, hogy bajok vannak az én formális logikai fordításommal. Gallois 2017-es, a változás lehetőségét taglaló álláspontját elemző részben lefordítom formális logikai nyelvre Gallois gondolatait. Rájöttem, hogy ezzel a fordítással gondok vannak. Ide másolom a korábbi szövegem vonatkozó részét, hogy érthető legyen hol látok hibát.
***
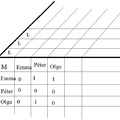
Def. Her(xyt1t2):= t1-beli x-nek a t2 beli y a leszármazottja
Def. Per(xt1t2):= x fennmarad t1és t2 tartományban
Def. Mod(xt1t2) := x megváltozott t1 és t2 tartományban
Az első argumentum:
(i) Miközben valami megváltozik, valaminek változatlannak kell maradnia a változás során.
(i.1)ExMod(xt1t2)->EyPer(yt1t2)
(ii) Ahhoz hogy valami fennmaradjon a változás során, az ugyanaz kell legyen a változás után, mint annak előtte volt.
(ii.1) Mod(xt1t2)& Per(xt1t2) -> Ey(Her(xyt1t2) & ER(Rxt1 &~Ryt2) & x=y)
A formula feltételezi, hogy valami változik, és ugyanakkor fennmarad.
(iii) De ahhoz, hogy valami megváltozzon, annak a változás után különböznie kell a változás előtti önmagától.
(iii) kétféle módon is érthető:
(iii.1) Mod(xt1t2)->ER(Rxt1 &~Rxt2)
(iii.2) Mod(xt1t2)->Ey(Her(xyt1t2) & x><y)
(iv) Semmi sem lehet egyszerre ugyanaz és különböző.
(iv) is kétféle módon is érthető:
(iv.1)~ExEt (Rxt &~Rxt)
(iv.2)~ExEy(x=y & x><y)
***
Baj van a definíciókkal. Az első definíció értelmezési tartománya különbözik a másik kettő értelmezési tartományától. Az első definíció így szól:
Def. Her(xyt1t2):= t1-beli x-nek a t2 beli y a leszármazottja
Mik a lehetséges értékei x és y változóknak? Vajon x és y értékei fizikai tárgyak endurantista (3D) felfogásban, vagy ettől eltérően fizikai tárgyak perdurantista (4D) felfogásában lévő idő szeletek vagy stage-k? Ha én leszármazottja vagyok az egy évvel korábbi önmagamnak, és az egy évvel ezelőtti önmagam ’a’, a mostani pedig ’b”, akkor vajon igaz-e, vagy sem, hogy a=b? A tagadó válaszra hajlok. Mindkettő én vagyok abban az értelemben, hogy önmagam különböző időpontokban való megjelenését jelenti ’a’ és ’b’. A kettő azonban nem azonos, mert eltérő tulajdonságai vannak. Ha a korábbi időpont t1, és a későbbi t2, akkor ezt így fejezhetjük ki:
a = önmagam(t1)és b=önmagam(t2).
Ezek alapján a ’Her’ predikátum első két argumentum helyeinek értékei tárgyak időszeletei, vagy stage-i. Ha a két időszelet különböző tárgyakhoz tartozik, akkor nem áll fenn a reláció, ha egyazon fizikai tárgyhoz, akkor igen. A másik két definíció nem vet föl ilyen kérdést, azok a tárgyak szokásos, endurantista felfogásában értelmezettek.
Baj van a (ii.1) formulával. Lássuk, hogy miért. A (ii.1) formula (ii)-t kívánta kifejezni.
(ii) Ahhoz hogy valami fennmaradjon a változás során, az ugyanaz kell legyen a változás után, mint annak előtte volt.
(ii.1) Mod(xt1t2)& Per(xt1t2) -> Ey(Her(xyt1t2) & ER(Rxt1 &~Ryt2) & x=y)
Azonban a (ii.1)-ben lévő kondicionális előtagjában szereplő x endurantista értelemben fogja föl a fizikai tárgyakat, de a kondicionális utótagja nem így értelmezi. Tehát eltérő az előtag és utótag értelmezési tartománya. Ha x és y egy tárgy egymást követő állapotai, ahol a tárgy megváltozik, akkor a két állapot nem lehet azonos. A formula egy javítása lehet az alábbi:
(ii.1.javított) Mod(xt1t2)& Per(xt1t2) -> Ex(Her(uwt1t2) & ER(Rut1 &~Rwt2 & u=x(t1) & w=x(t2))
Ebben a megfogalmazásban a két időpont a tartomány szélére esik, de átfogalmazható úgy is, hogy a szélső értékek közé essen.
Baj van a (iii.2) formulával is. A kondicionális utótagja hibás. Helyesen így fest:
(iii.2.javított) Mod(xt1t2)->ExEuEv(Her(uvt1t2) & u><v & u=x(t1) & v=x(t2))