Három dolgot fontos megértenünk a Yablo paradoxonról:
1. A paradoxon megfogalmazható az igazság predikátum használata nélkül is. Az eredeti sorozat így festett:
(S1) minden k>1 –ra, Sk nem igaz
(S2) minden k>2 –ra, Sk nem igaz
(S3) minden k>3 –ra, Sk nem igaz
.
.
A sorozat folytatására utaló pontok is így fordultak elő az eredeti cikkben. Figyeljük föl arra a pongyolaságra, hogy a formulák nevei, melyek a bal oldali zárójelbe tett jelek, maguk is részei a formuláknak. Ezek után fogalmazzuk meg másképp a gondolatmenetet. Legyenek n, k természetes számok (n = 0, 1, 2 …), ekkor megszerkeszthetjük a Yablo mondatsorozatot az alábbi módon:
(Y0) S(0) « "k. 0 < k® ~S(k)
(Y1) S(1) « "k. 1 < k® ~S(k)
(Y2) S(2) « "k. 2 < k® ~S(k)
…
(Yn) S(n) « "k. n < k® ~S(k)
(Yn + 1) S(n + 1) « "k. n + 1 < k ® ~S(k)
Most a formulák nevei nem részei a formuláknak, és a formulák elsőrendűek, és nem használják az ‘igaz’ szemantikai predikátumot. Belátható, hogy a Yablo paradoxon S(n) sorozata következménye egy másodrendű logikai formulának:
(Ya) $s"n: n természetes szám ® ( s(n) « "k (n < k ® ~s(k)))
2. A paradoxon csak látszólag kapcsolatos a logikával, annak alapjaival. Valójában logikai fogalmak nélkül is megfogalmazható, pl. kalapokkal vagy számokkal. Vegyük az utóbbit. Legyenek érvényesek a szokásos aritmetikai igazságok (AR); és f kétértékű függvény értéke akkor és csak akkor 1 valamilyen n számra, ha minden n-nél nagyobb számra f értéke 0. Ezek után ezt kapjuk:
(Y0) 1 = f(0) « "k. 0 < k® 0 = f(k)
(Y1) 1 = f(1) « "k. 1 < k® 0 = f(k)
(Y2) 1 = f(2) « "k. 2 < k® 0 = f(k)
…
(Yn) 1 = f(n) « "k. n < k® 0 = f(k)
(Yn+1) 1 = f(n + 1) « "k. n + 1 < k ® 0 = f(k)
Az antinómia ekkor így vezethető le:
*(1) 1 = f(n) feltételezzük, hogy f értéke n-re 1
*(2) "k. n < k® 0 = f(k) (Yn)
*(3) n < n + 1® 0 = f(n + 1) (2)
*(4) n < n+1 (AR)
*(5) 0 = f(n + 1) (3) (4)
*(6) ("k. n < k® 0 = f(k) ) ® ( "k. n + 1 < k ® 0 = f(k) ) (AR)
*(7) "k. n + 1 < k ® 0 = f(k) (2) (6)
*(8) 1 = f(n + 1) (7) (Yn + 1)
(9) 1 = f(n) ®. 0 = f(n + 1) & 1 = f(n + 1) (1) (5) (8)
(10) 0 = f(n) (9)
(11) "n. 0 = f(n) (10) n tetszőleges volt, ezért univerzális általánosítással
(12) "k. n < k® 0 = f(k) (11) (AR)
(13) 1 = f(n) (Yn)
(14) 0 = f(n) & 1 = f(n) (10) (13)
Az ellentmondás eltűnik, ha a sorozat tárgyalási univerzumát kiegészítjük egy transzfinit számmal, pl. w-val, amely transzfinit szám nagyobb minden természetes számnál.
Tegyük fel, hogy 1 = f2(w) és 1 = f2(n) « "k. n < k® 0 = f2(k)
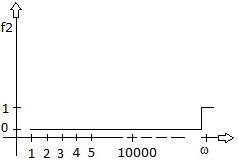
3. Mit jelent jelen esetben a paradoxon? Azt jelenti, hogy feltételeztük valaminek a létezését, de ez a feltevés ellentmondásra vezet. Mi következik ebből? Az következik, hogy el kell vessük a feltételezésünket, a sorozat, melynek létezését feltételeztük, valójában nem létezik. Fontos ezt jól érteni. Nem a jelek sorozata létezését tagadjuk, hiszen a papír bármit elvisel, hanem a logikai formulák egy adott sorozatának a létezését, amely sorozat minden tagja konzekvensen igazra vagy hamisra értékelhető. Az un. paradoxon abból fakad, hogy egy különös rekurzív sorozatnak nem adtuk meg a bázisát. Amint megadjuk, az ellentmondás, a paradoxon elillan, még akkor is, ha végtelen sok tagja van. Mivel hiányzik egy rekurzív sorozat bázisa, a sorozat meghatározása körbeforgó, azaz hibás. (Stephen Yablo nem tartja a körbeforgó definíciókat feltétlen hibásnak, sajátos, érdekes elmélete van ezzel kapcsolatban, de erre itt most nem térhetek ki.)
A sorozat véges szelete fölírható numerikus formában, úgy, hogy táblázatkezelővel is kiszámolhatjuk. Ekkor az univerzális kvantor helyett soktagú összeget használhatunk.