Bevezetés

A piszkavasnak fontos filozófiatörténeti jelentősége van. Állítólag ezzel ijesztgette Ludwig Wittgenstein Karl Poppert egy nyilvános előadáson érveinek nagyobb nyomatékot adandó.

1946. október 25-én Karl Poppert meghívták előadni a „Léteznek-e filozófiai problémák?” c. cikkéről a Cambridgei Erkölcs-filozófiai Tudományok Klub találkozóján, aminek Ludwig Wittgenstein volt az elnöke. Ezek ketten hevesen vitatkozni kezdtek, hogy valóban léteznek-e alapvető filozófiai kérdések, vagy csupán nyelvi rejtvényekből áll a filozófia – utóbbit Wittgenstein képviselte. Wittgenstein egy piszkavassal hevesen gesztikulálva bizonygatta igazát a mind hevesebbé váló vitában. Végül Wittgenstein Poppernek szögezte a kérdést: mondjon nekem csak egyetlen bizonyos morálfilozófiai tételt! Popper így felelt: „Nem illik a vendég előadót piszkavassal ijesztgetni!” Erre Wittgenstein lecsapta a piszkavasat és elviharzott. A történet pikantériájához tartozik, hogy miközben számos szemtanúja volt a történteknek, és a közönség olyan híres filozófusokból állt, mint Bertrand Russell, akik mindenki másnál többet tudnak az igazság természetéről, senki sem biztos abban, hogy mi történt. Van, aki szerint így történt, van, aki szerint Wittgenstein nem fogott a kezébe semmiféle piszkavasat, van, aki szerint a replikát csak utólag találta ki Popper.

Utóbb könyvet is írtak a mókás esetről.[1] Ennél fontosabb, hogy Bertrand Russell a piszkavas időbeli melegedési függvényével próbálta az időbeli változás fogalmát bemutatni vitapartnerének, McTaggartnak. McTaggart képtelen volt fölfogni a modern matematikai-fizika szemléletmódját – nem volt egyedül, ma se lenne egyedül – Russell viszont nem értette meg, hogy mi a filozófiai probléma az idő fogalmával. Mi most kicsit alaposabban megvizsgáljuk ezt a piszkavas kérdést – az időt most békén hagyjuk, múljon csak kedvére. Hogy is van ez a melegedés? És hogy lehetne ezt leírni egyszerű, de mégis precíz matematikai nyelvezettel, és modellálni egy véges automatával? Utóbbi modellt a későbbiekben a „szükségszerűség” fogalma explikálására fogom fölhasználni. 

Példa 2.

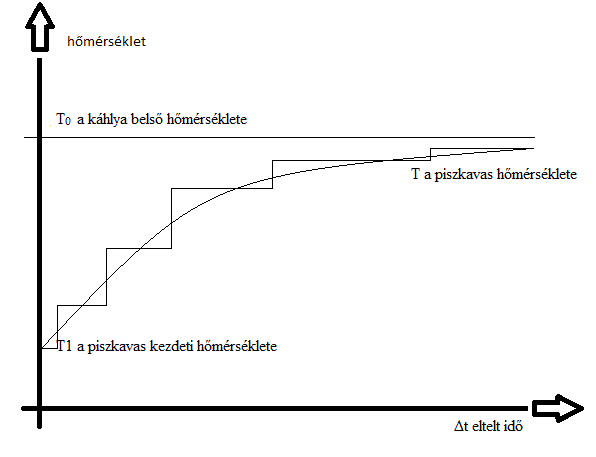
Tegyük fel, hogy a kályha, amelyben egy piszkavasat melegítünk, a folyamatos energiatermelés miatt végtelen hőkapacitásúnak tekinthető (a piszkavashoz képest), azaz állandó hőmérsékletű a kölcsönhatás során. Ekkor a piszkavas melegedése a T(Δt)=T₀-T₁*e^–k*Δt képlettel írható le, ahol: T a piszkavas pillanatnyi hőmérséklete, T₀ a kályha belső  hőmérséklete – ez egyben a piszkavas környezete amikor a tűzbe tesszük – T₁ a piszkavas kezdeti hőmérséklete, k a piszkavas hőtani, felületi és a környezet hővezetési adataiból alakuló állandó, Δt a kölcsönhatás kezdetétől eltelt idő, és ’e’ az Euler féle szám.[2] 

(1)  T(Δt)=T₀-T₁*e^–k*Δt

 A piszkavas fokozatosan melegszik föl egy maximális értekre, miután a tűzbe tettük. Vannak hatások, amelyek egy kísérleti elrendezésre azonnal hatnak, más rendszerekre a környezet fokozatosan fejti ki hatását. Ezt a különbséget az analóg automaták (fekete dobozok) két csoportja fejezi ki: a nem tárolós illetve a tárolós átviteli tagok. Előbbieken a hatás – a bemeneti jel – késleltetés nélkül áthalad, az utóbbiakon viszont időben eltolva, és csak fokozatosan érvényesül a hatása. Magát a jelenséget különböző pontossággal írhatjuk le. Ábrázolhatjuk a valós számok tartományán analóg jellel, vagy az egész számok, vagy hányadosaik tartományán, digitális jellel. Ezt a két lehetőséget mutatja a piszkavas alábbi melegedési grafikonja. 

Figure 1

A példa filozófiai vonatkozásai

A piszkavas melegedése számos érdekes filozófiai kérdést vet föl: 

1. Miközben fölforrósodik, megváltozik a színe – a vége izzani kezd – és mivel kitágul, kis mértékben az alakja is megváltozik. Miért mondjuk mégis, hogy eközben megtartja önazonosságát, hiszen mások a tulajdonságai hidegen, mint forró, izzó állapotban? Egyáltalán le lehet ezt a változást ellentmondásmentesen írni? Mi a piszkavas, van-e benne valami állandó, miközben változik?
2. A piszkavasnak az a tulajdonsága, hogy fokozatosan melegszik és hűl le, nem pedig azonnal, késedelem nélkül, nem alkalmi, esetleges tulajdonsága a piszkavasnak, hanem minden esetben ez történik vagy történne. Még akkor is, ha soha nem tesszük a piszkavasat a tűzbe. Ezt a hitünket úgy is kifejezhetjük, hogy szükségszerűen igaz, hogy a piszkavas, mint fekete doboz, vagy mint automata, tárolós átviteli tagot képvisel.
3. Mit jelent a ’lehetőség’ és ’szükségszerűség’ a piszkavas melegedése esetén? Vajon csak az a lehetőség a piszkavas melegedését vagy kihűlését számba véve, ami valamikor bekövetkezik, vagy a lehetőség ennél többet jelent? 

Számtalan módon fölmelegedhet és lehűlhet a piszkavas attól függően, hogy milyen meleg a kályha, de nem bármilyen módon. Ezért számtalan, az ábrához hasonló függvénygörbe írja le a piszkavas összes lehetséges melegedését és lehűlését, de nem bármilyen görbe. A görbe meredekségét korlátozza a piszkavas tömege és anyagminősége. Hogy ne akadályozzanak a matematikai végetlennel kapcsolatos nehézségek, a piszkavas melegedését és lehűlését, azaz a piszkavas történetét közelítő pontossággal, lépcsőzetes grafikonokkal írjuk le, és az időnek csak egy véges T tartományával foglalkozunk. Így is nagyon nagyszámú lesz a piszkavas összes lehetséges hőmérsékleti grafikonja, de nem végtelen, mert az időt is diszkrét időpontok, ütemek sorozataként fogjuk fel. Ez lehetővé teszi, hogy a piszkavasat ne csak analóg automatákkal, hanem diszkrét időben működő és csak véges sok állapotú, véges automatákkal is szimulálhatjuk. 

Modális fogalmak egy alternatív értelmezése

A piszkavas összes lehetséges melegedési vagy kihűlési függvényét jelölje Ψ, ennek egy eleme a piszkavas valóságos történetét leíró φ_reality függvény, amelyet azonban csak részben, a jelen pillanatig ismerünk. Ψ létezik, mivel (1) egyenlet alapján meghatározható, ugyanis véges T tartományra, az egyszerűsítő feltételek mellett, minden eleme a megadott képlet alapján kiszámolható. (A számítást gép is elvégezheti.) A jelen pillanatig tartó φ₀ függvény -- a piszkavas eddigi melegedése vagy kihűlése -- azonban szintén eleme Ψ-nek, mert egy a lehetséges függvények közül. Ψ-nek azt a szűkítését, amelyik pontosan azokat a függvényeket tartalmazza, melyek a jelen időpontig megegyeznek a piszkavas történetével, utána viszont az összes lehetséges melegedési vagy kihűlési függvényt tartalmazzák, Ψ^w0-val jelölöm. φ₀ a jelen időpontig tartó szelete φ_reality függvénynek. Lehetőség a jelen időpontban egy olyan φ_i függvény, amelyik eleme Ψ^w0-nek. Mind Ψ, mind Ψ^w0 a megadott fizikai képlet alapján meghatározható az egyszerűsítő feltevések mellett. Tömören összefoglalva mindezeket a halmazelmélet nyelvén így fejezhetjük ki, ahol t₀ := jelen-időpont, w₀ pedig a t₀ időponthoz tartozó piszkavas állapot: 

(2) Ψ^w0⊆Ψ és φ₀∈Ψ^w0 és φ_reality∈Ψ

(3) |Lehetséges(φ_i)| _w0:= φ_i∈Ψ^w0 

Figyeljük meg jól, hogy ebben a felfogásban lehetőség az, ami valamilyen környezeti hatást feltételezve levezethető a piszkavas melegedési egyenletéből, szükségszerűen igaz pedig az a piszkavasra vonatkozó fizikai kijelentés, amelyik a melegedési egyenlet alapján az összes lehetséges környezeti hatás esetén is igaz. A piszkavas melegedési egyenletét azonban valamiképp logikai nyelven kell megfogalmazzuk, hogy szabatos filozófiai állításokat tehessünk. Erre szolgál a piszkavas viselkedését szimuláló véges automata modell. Ilyen módon fogom visszavezetni a piszkavasra vonatkozó némely fizikai kijelentés szükségszerű igazságát a piszkavas tulajdonságaira. Hiszen szükségszerű, hogy a piszkavas késleltetve melegszik föl, és késleltetve hűl le. Ennek megértéshez nem kell a lehetséges világokban létező hasonló piszkavasakban hinnünk, ahogy David Lewis állítja. 

A fenti meghatározások szerint csak egy jövőbeli esemény lehet kontingens, a jelen és a múlt szükségszerű, és érvényes a következő két feltevés:

(17) Minden ami elmúlt lehetséges, mert megtörtént, és szükségszerű, mert megtörtént és nem lehet meg nem történtté tenni. Mivel a jelen is megtörtént, és a múlthoz hasonlóan nem lehet meg nem történtté tenni, ezért a jelen is szükségszerű;

(18) Egy jövőt leíró mondat lehetséges, hogy igaz, ha a jelenből kiindulva van a körülményeknek olyan alternatívája, amely igazzá teszi. Egy jövőt leíró mondat szükségszerű, hogy igaz, ha a jelenből kiindulva a körülmények minden alternatívája igazzá teszi. 

A piszkavas modellje innen letölthető:

http://ferenc.andrasek.hu/modellek/poker-hu.xls

A győzedelmes argumentum cáfolata

(17) és (18) igazolja, hogy az alábbi Diodórosz Kronosznak[3] tulajdonított, sokak által ellentmondásosnak vélt három állítás a fenti keretrendszerben kielégíthető, tehát nem tartalmaz ellentmondást: 

(A) A múltra vonatkozó minden igaz kijelentés szükségszerű.

(B) Lehetséges kijelentésből logikailag nem következik lehetetlen kijelentés.

(C) Egy jövőre vonatkozó kijelentés, amely nem igaz, még lehetséges, hogy igaz. 

Mutassuk meg a fenti három mondat kielégíthetőségét egy modell megadásával.

A piszkavasat nappal t_-5 időpontban vettem, amikor is hideg volt és fekete színű. A mai napig csak kétszer tettem egy pillanatra a tűzbe, így mostanáig nem volt forró, csak meleg t_-4 és t_-2 időpontokban. Most - t₀ időpontban - épp meleg, mert rövid ideig a tűzben volt, de tegyük fel, hogy a jövőben többet nem használom, így hideg marad. Igazolható-e a korábban bemutatott piszkavas automata modell segítségével, hogy mégis lehetséges, hogy forró lesz valamikor?

φ_reality sorozatot az alábbi táblázat mutatja. (A piszkavas színeitől most eltekintettem.)

3. táblázat φ_reality

φ₀ ennek egy részlete:

4. táblázat

φ₁ az alábbi sorozat:

5. táblázat

(A )A modell alapján belátható, hogy φ₁∈Ψ. Mivel φ₁–nek kezdő sorozata φ_0, ezért φ₁∈Ψw0. Vegyük azt a mondatot, hogy a piszkavas hideg t_{-1 -}kor. Ez egy múltra vonatkozó állítás, amely φ _reality alapján igaz. Vajon szükségszerűen igaz-e? Mivel ezt a mondatot φ₀ önmagában is igazolja, ezért Ψw0 minden eleme igazolja, tehát a ’piszkavas hideg t_-2 kor’ mondat szükségszerűen igaz. Nyilvánvalóan erre következtetnénk más múltbeli vagy jelenbeli igaz mondatok esetén is. Ezzel (A) igazolást nyert.

(B) Tegyük fel, hogy q lehetséges, q kijelentésből következik p, és p lehetetlen kijelentés.  Ha p lehetetlen kijelentés, akkor nincs olyan φ_i∈Ψw0 függvény (állapot sorozat), melyből p az automata modell segítségével levezethető, mivel a modell konzisztens. Viszont q kijelentésből levezethető p, ezért ha nincs olyan φ_i∈Ψw0 amiből p levezethető, akkor nincs olyan akkor φ_j∈Ψw0 amiből q levezethető. Ekkor azonban q lehetetlen, mert nincs olyan φ_jÎΨw0 amiből q levezethető. Ez ellentmond a kiindulásunknak, hogy q lehetséges, tehát el kell vessük a feltevést. Mivel p és q tetszőleges mondat volt, ezzel (B) is igazolást nyert.

(C) Most vegyük azt a mondatot, hogy a piszkavas forró t₃-kor. Ez hamis φ_reality szerint, viszont igaz φ₁-ben. Ekkor viszont van olyan eleme Ψw0-nak ami igazolja, hogy a piszkavas forró lehet t₃-kor, miközben valójában nem forró t₃-kor. Nyilvánvalóan erre következtetnénk más jövőbeli igaz φ_i∈Ψw0 mondatok esetén is. Ezzel (C) igazolást nyert. Figyeljük meg, hogy a két mondat esetén a szükségszerűség relatív a jelenhez (t₀-hoz) képest. A jelent hátrább tolva ’a piszkavas meleg t_-2 kor’ mondat szükségszerűből esetlegessé válik, és előre tolva, ’a piszkavas forró t₃-kor’ mondat lehetségesből lehetetlenné válik.[4]

Zárszó

Logikai szempontból a szükségszerűség most bemutatott felfogása Carnap felfogásának egyfajta értelmezése és továbbgondolása. Ebben a felfogásban a szükségszerűség keretrendszerhez kötött, és nem operátor, hanem metanyelvi predikátum, így nem iterálható triviálisan. Nincs szükség a modellek által leírt tárgyakon kívüli lehetséges világok feltételezésére, mert a lehetséges világokat lehetséges állapotoknak tekintve redukáltuk az automaták belső és külső állapotai halmazára. Ilyen módon az automaták által szimulált fizikai tulajdonságok két dolgot tesznek értelmezhetővé: 

(19) a tulajdonságok a modellekhez kötötten léteznek, azok lehetséges állapotai, ami filozófiai szempontból azt jelenti, hogy a fizikai tulajdonságok a tárgyakhoz kötötten léteznek, nem pedig mint önálló létezők;

(20) a tulajdonságok terjedelme nem korlátozódik azokra az értékekre amelyeket a tárgyak aktuálisan fölvesznek vagy fölvettek, hanem kiterjednek az összes lehetséges értéke. Ez azért van így, mert a működést meghatározó összefüggések az összes lehetséges állapot közötti átmenetet határozzák meg, nem csak az aktuális állapotokat. Így magukba foglalják az összes lehetséges állapot halmazát, és az egyes állapotok a tulajdonságok leképezései. 

Ha azonosítjuk a tárgyakat tulajdonságaik összefüggéseivel, akkor az úgy jelenik meg ebben a felfogásban, hogy a tárgy azonos az őt szimuláló modellel. Ez megválaszolja a fizikai tárgyak önazonossága kérdését is. A tárgy bár változik, a belső összefüggései, ahogy a környezeti hatásokra reagál, változatlanok, és a működési szabályai alapján megjósolhatóak az aktuális tulajdonságai a különböző környezeti feltételek között.

A teljes szöveg innen tölthető le:

http://ferenc.andrasek.hu/blog/piszkavas.pdf

 Jegyzetek

[1] David Edmonds, John Eidinow, „Wittgenstein's Poker: The Story of a Ten-Minute Argument Between Two Great Philosophers” (2002) a könyv ismertető a netről van.

[2] A kísérlet fizikai magyarázatáért köszönettel tartozom Zimmermann Pál fizikusnak.

[3] Diodórosz Kronosz görög filozófus. A káriai Iaszoszból származott, Ptolemaiosz Szótér udvarában élt. A megarai iskolához tartozó filozófus és nyelvész volt. Említi Diogenész Laertiosz, Sztrabón és Cicero, munkái nem maradtak fenn. Wikipédia

[4] Egy ezzel ellentétes álláspont: Altrichter Ferenc, „A győzedelmes argumentum” in. Észérvek az európai filozófiai hagyományban (1993) Atlantisz, Bp.