Korábban ígértem, hogy visszatérek ehhez a kérdéshez. Mindenekelőtt rögzítsük, hogy mi is az a tézis, amit vitatok. Tegyük fel, hogy tudjuk, mit jelent fizikai tárgynak lenni, mik a fizikai tárgyak. Hasonlóképpen azt is tudjuk, mit jelent fizikai eseménynek lenni, mik a fizikai események. Utóbbi két kijelentés szétválasztja az objektumokat, fizikai tárgyakat és az eseményeket, fizikai eseményeket. Tudatában vagyok annak, hogy ez a szétválasztás már önmagában is számos kérdést vet föl, most mégis azt javaslom, hogy ezen emelkedjünk felül és most ne foglalkozzunk az eseményekkel, csak a téridőben folyamatosan létező dolgokkal, objektumokkal, pontosabban fizikai tárgyakkal. Tehát olyan dolgokra gondolok, melyek térben és időben folyamatosan léteznek. Ezek alapján – tehát az események univerzumát most kihagyva – a naiv fizikalizmus tézise, amit elemezni fogok, így szól:

(1) Minden fizikai tárgy.

Ennek valamivel bőbeszédűbb megfogalmazása ez lenne:

(1’)Minden dolog fizikai tárgy.

Vagy még terjengősebb megfogalmazásban:

(1’’) A világon minden dolog fizikai tárgy.

Utóbbi arra utal, hogy a mesék, mítoszok világában, vagy az álmok világában létezhetnek extra fizikai dolgok, de a valóságban, azaz a világon nem, ott csak és kizárólag fizikai tárgyak vannak. Ezt nem úgy értendő, hogy mindennek ami létezik fizikai természete is van, hanem úgy, hogy nincs másfajta természete, csak és kizárólag fizikai. Nincsenek pl. számok, azok csak egy képes beszéd szófordulatai, számok valójában nem léteznek. Ami mellet érvelni szeretnék az éppen az, hogy ez a ’valójában’ szófordulat félrevezető, megtévesztő, és gondokat okoz. 

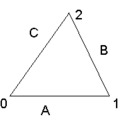
Aki középiskolát végzett annak számára belátható, hogy 1=sin(π/2) és az is, hogy 0 < cos(0). Ezeknek az iskolában tanult formuláknak az igazságát, vagy helyességégét, egyszerű geometriai ábrákkal szokták elmagyarázni.  Az ábrák jelentést kölcsönöznek a formuláknak, és megindokolják elfogadásukat. Olyan nyilvánvalóságokat hogy 1=1, vagy 0 < 1, még ezen az iskolás szinten sem szokás tárgyalni, annyira egyszerű és nyilvánvaló igazságok ezek. Ha ezeket nem értené valaki, vagy komolyan kételkedne az igazságukban, annak kétségbe vonnák a normális elme állapotát. Filozófusként, most mégis ezt tesszük. Hogyan is állunk azzal mondattal, hogy 1=1?

Aki érti az ’azonos’ szó fogalmát és tisztában van a Vénusz égitest két másik nevével, annak számára nyilvánvaló igazság, hogy az esti csillag = hajnal csillag. Azért igaz ez, mert az ’esti csillag’ és a ’hajnal csillag’ nevek egyazon dolgot neveznek meg. Mi a helyzet azonban az 1 = 1-el mondattal? Ha fizikalisták vagyunk, és hiszünk a fenti (1) tételben, akkor ezt elutasítjuk, mivel nem hiszünk a számok létezésében, olyan dolgokéban, melyet az ’1’ jel megnevez. Fizikalistaként szerintünk csak fizikai tárgyak vannak, márpedig jól látható, hogy valami van az ’=’ jel bal oldalán, és valami van a jobb oldalán, de ami két különböző helyen van, az nem lehet egymással azonos, lásd a Vénusz két megnevezését. Valójában fizikalistaként nem csak a számok létét, de a jelek létét is tagadjuk, hiszen a jelek is absztrakt objektumok, nem pedig fizikai tárgyak. Az azonosság jel két oldalán az iménti példában két különböző jelpéldány van, és nem egyazon jel két előfordulása. Fizikalistaként csak azt fogadjuk el, hogy az azonosság jel valójában egyformaságot vagy hasonlóságot állít, és nem az azonosság jel két oldalán lévő fizikai tárgyak, azaz jelpéldányok azonosságát. Eddig rendben is volnánk.

Mi a helyzet azzal a mondattal, hogy 0 < cos(0)  azaz 0 < 1? Hogyan értsük azt, hogy a  ’0 < cos(0)’ mondat matematikailag egyenértékű, azaz felcserélhető a ’0 < 1’ mondattal? És egyáltalán, fizikalistaként hogyan értendő a ’0 < 1’ mondat? Talán arra gondolunk, hogy a ’0’ jelpéldány kisebb mint az ’1’ jelpéldány? Milyen értelemben? Hiszen a magasságuk egyforma, az általuk elfoglalt helyre pedig nem igaz az állítás, hiszen látható, hogy a ’0’ fizikai tárgy nem foglal el kevesebb helyet, mint az ’1’ fizikai tárgy. A fő baj azonban a fizikalizmussal teljesen általános természetű. Arról van szó, hogy bár a nyelv használata jelpéldányok használatát jelenti a térben és időben, maga a nyelv azonban jel atomokból és nem jelpéldány atomokból áll. Valóban jelpéldányokat használunk, de ezeket jeleknek tekintjük és nem egyszerű fizikai tárgyaknak, melyek csak és kizárólag önmaguk előfordulásaival azonosak.

Tényszerűen nem igaz, hogy az elemi iskolában tanult számtan értelmetlen jelsorozatok bemagolásából áll. Tényszerűen nem igaz, hogy az aritmetikai állítások jelentés nélküliek – E. Szabó László felfogásából ez következik. A naiv fizikalista nem mond igazat, amikor azt állítja, hogy nem hisz a számok létezésében. A naiv fizikalista akkor sem mond igazat, amikor jelek helyett jelpéldányokról beszél, és kétségbe vonja a jelek és a nyelv, mint absztrakt létezők létét. Ezeket ő is használja, ha igaza volna, nem tudna beszélni sem számolni.

Amit a fizikalizmus állít, az csak akkor értelmes, ha nem vonatkozik önmagára, máskülönben a beszéd puszta jelentésnélküli zaj, az írás meg értelmetlen alakzatok sorozata. (Hasonló igaz az okság és a természeti törvény fogalmára is. Ha gépek vagyunk, akkor az igazság fogalma elenyészik. Ezt pl. Thomas Nagel is jól látta az Utolsó szó c. könyvében.)  Amit a fizikalizmus mondani akar, az a világon belülről nem állítható, belülről csak puszta hangzavar. A fizikalizmus csak a világon kívülről fogalmazható meg értelmesen, amikor feltételezzük, hogy belülről nézve gondolkodó, szabad lények vagyunk, aki gondolataikat nyelv segítségével fejezik ki.