Bevezetés

Egyszerű fizika példákkal jobban lehet bemutatni filozófiai problémákat, mint köznyelviekkel, mert a fizika lehetővé teszi a történések szabatos, ám egyszerű matematikai nyelven történő leírását. Az olyan események említése filozófiai magyarázatok összefüggésében, mint Caesar meggyilkolása, egy árvíz vagy egy robbanás bekövetkezése, ezen események komplexitása miatt számos homályosság és kétértelműség forrása. Így eltereli a figyelmet a filozófiai problémák lényegéről. Ezzel szemben egy kocsi mozgása vagy egy piszkavas melegedése, olyan események, melyek jól leírhatók formulákkal, és nem indukálnak meddő vitákat arról, hogy mi az ’esemény’ fogalma, mi az, amiről beszélünk.  

Következő példáim a fizika nézőpontjából nagyon egyszerűek. A fő kérdés, amit a példák kapcsán több oldalról megvizsgálunk, ami a különféle metafizikai szekértáborok közötti határvonalat kijelöli: elköteleződés az ontológiai kategóriák valamilyen rendszere mellett. Az is erről szól, ha valaki a metafizikai megfontolások létjogosultságát általában tagadja.

Példa 1.

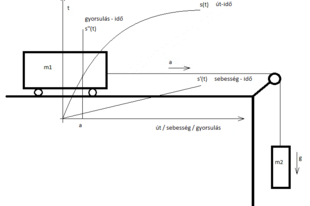
Vízszintes, egyenes pályán gördülő kocsi tömege m₁. A kocsit egy kötél húzza előre oly módon, hogy a sínpálya végén, egy csigán átvetve lóg a mélybe a másik vége, melyen egy m₂ tömegű súly lóg. Ez a súly húzza előre a kocsit ’a’ gyorsulással.[1]

Meghatározandó az ’a’ gyorsulás értéke a következő egyszerűsítő feltételekkel:

(a) a kocsi, a kötél és csiga súrlódási ellenállása valamint a levegő ellenállása elhanyagolható;

(b) a kötél nagyon erős, nem nyúlik, de nem is szakad el, könnyen hajlik, és tömege elhanyagolható;

(c) a testekre ható nehézségi gyorsulás, amelyet ’g’-vel jelölök, állandó, nem függ a súly helyzetétől, magasságától;

(d) a rendszerre nem hat más erő, pl. nincs a közelben erős mágnes vagy fénynyomás;

(e) a rendszer alkotóelemei, a kocsi és a súly, szilárdak, nem esnek ki belőlük darabok;

(f) a newtoni klasszikus fizikában gondolkodunk, a kísérlet során adott egy inercia rendszernek tekinthető vonatkoztatási rendszer.

 Ezek nagyon erős leegyszerűsítések. Viszonylag könnyű lenne figyelembe venni a kocsi és a csiga súrlódását, de gyorsulás közben a kötél tömegének a változó aránya tartozik az egyik illetve a másik tömeghez, és ez már bonyolulttá tenné a formulát. A kocsi tömege nyilvánvalóan nem lehet nagyon kicsi, pl. atomi, vagy nagyon nagy pl. csillagászati objektum méretű, ahol tökéletesen más fizikai törvények működnek, mint amit most feltételezünk.

A két tömeg egyszerre mozog, gyorsulásuk egymásra merőleges irányú, de a kocsi és a súly gyorsulását kifejező skaláris értékek megegyeznek, mert a kötél nem nyúlik meg. A kocsit előre húzó nehezék mindkét tömeget gyorsítja, ezért a gyorsulás az alábbiak szerint számítható ki Newton második törvényét alkalmazva:

 (1) a * (m₁ + m₂) = g * m₂    

(2) a = g * m_{2 /} (m₁ + m₂)      

(3) a/g = m₂ / (m₁ + m₂)         még világosabban:

(4) a/g = 1 / (1+m₁/m₂)

Figyeljük meg mit mondanak nekünk a formulák. Ha a kocsi tömege nulla vagy nagyon kicsi, illetve ha a súly tömege sokkal nagyobb mint a kocsi tömege, akkor a gyorsulás a nehézségi gyorsulással lesz közel egyenlő. Ha viszont a súlyt leakasztjuk, azaz amikor a súly tömege nulla, akkor a kocsi meg sem mozdul, tehát a gyorsulás értéke is zérus. A második formulát átírjuk annak a figyelembevételével, hogy a gyorsulás nem más, mint a helyváltozás- mértékének (vagyis a sebességnek) változása. Matematikai nyelven fogalmazva: a gyorsulás a kocsi út-idő függvényének második deriváltja. (Az első derivált a sebesség.) Tehát a kocsi sebessége az idő függvényében: s’(t) ahol, s(t) a kocsi sínen mért helye az idő függvényében, a kocsi gyorsulása pedig a második derivált, azaz s’’(t).

A második formula ezek alapján így alakul:

 (5) s’’(t) = g * m_{2 /} (m₁ + m₂)  ahol a= s’’(t)

 Innen az ismert módon következik a sebesség és út függvénye:

 (6) s’(t) = a * t

(7) s (t) = ½ * a * t²

Az alábbi ábra segít megérteni az eddigieket:

1.ábra

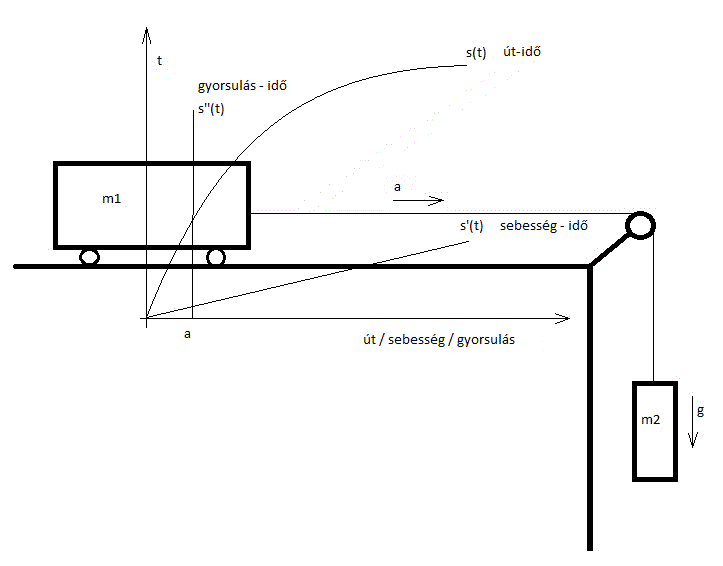
Mindez elég a fizikus számára, a filozófiában viszont központi jelentőségű a metafizikai-logikai tisztaság, hogy milyen fajta létezőről beszélünk, és minek a létezését tételezzük fel. Ezért ezek a formulák a filozófia céljaira nem elegendőek, mert a számszerű összefüggésekre fókuszálnak, és nem a létezés kérdéseire. Filozófiai nézőpontból van ugyanis két időben állandónak feltételezett objektumunk – a kocsi és a súly – melyeket logikai szempontból név típusú kifejezések jelölnek, a csigát és a kötelet elhanyagoltuk az egyszerűsítő feltevések megadása során. Azon kívül a következő fizikai jellemzők – mérhető mennyiségek – létezésében is hiszünk a két objektummal kapcsolatban: tömeg, idő, hely. Ezeket rendre a szokásos betűkkel, de a fizikától kicsit eltérő formulákkal fejezzük ki. Az eltérés lényege, hogy a fizikai jellemzőket – tömeg, hely – olyan függvényekkel írjuk le, amelyik minden egyes fizikai tárgyhoz megadják annak helyét és tömegét. A kocsit az egyszerűség kedvéért az ’k’, a súlyt a ’u’ individuumnév, a tömeget ’m’, a helyet ’s’ függvény jelek, az időt pedig ’t’ változó jelöli. Logikai-filozófiai nézőpontból azonban az ’m,s,t’ betűk nem egyszerűen fizikai változók, hanem objektumok, és az időpontok tartományán értelmezett függvények. Ezek alapján az ’k’ jelű kocsi helye t időpontban: s(k,t) a kocsi tömege m(k), a ’u’ jelű súly tömege m(u), és ’g’ az állandónak feltételezett nehézségi gyorsulás. Alkalmazva a jelöléseket, ezt a formulát kapjuk:

(8) s’’(k,t) = g * m(u) _/ (m(k)+m(u))

Természetes nyelven ez azt jelenti, hogy az ’k’-val jelölt objektum helyváltozás-mértékének változása egyenlő a nehézségi gyorsulás szorozva a második objektum tömegével, és osztva a két tömeg összegével.

A korábbiak alapján világos, hogy:

m₁=m(k)

m₂=m(u)

a = s’’(k,t)

Ezeket (8) formulába behelyettesítve visszakapjuk korábbi (2) képletet. Tehát (8) ugyanazt mondja mint (2), csak másképp. Ha általánosítani akarjuk a (8) formulát tetszőleges x és y objektumra és t időpontra, akkor ezt így fejezhetjük ki. Legyen Â(x,y):= x,y tömegek alkotórészei a kísérleti rendszernek az a,b,c,d,e,f határfeltételek között. Ezek alapján:

 (9) ∀x∀y∀t: ℜ(x,y) →. s’’(x,t) = g * m(y) _/ (m(x)+m(y))

(9) formula azt mondja, hogy ebben a kísérleti rendszerben, bármely x objektum gyorsulása konstans, melynek értéke az egyenlőségjel jobb oldalán lévő formulával számolható ki. Tetszőleges x kocsi helyét y súly esetén az alábbi formula írja le a t időpont függvényében:

 (10) ∀x∀y∀t. ℜ(x,y) →s(x,t) = ½ * g * m(y) _/ (m(x)+m(y)) * t²

Mire használhatók a formulák?

Arra, hogy előre megjósoljunk egyedi eseményeket, azt, hogy miképp fog mozogni a kocsi. A kocsi mozgását azután utólag megfigyelhetjük, és összevethetjük a formulából kiszámított értékkel. A formula lehetővé teszi, hogy akár a jövőbeli, akár a múltbeli eseményekre következtessünk a kísérleti elrendezés határai között. A formula ebben az értelemben megelőzi az egyedi tapasztalatot. Ugyanakkor a formula egyáltalán nem logikai-matematikai, kibernetikai vagy nyelvhasználatot leíró igazság, a formula tehát nem analitikus igazság.[2] A formula természeti törvényt fogalmaz meg, ami egyedi eseményeket jósol általános érvénnyel.

Mit jelentenek a korábbi fizikai formulák?

Közelítsük meg a jelentést, az igazságfeltételek nézőpontjából. Igaz-e a gyorsulást meghatározó (2) vagy (8) formulánk, vagy csak hasznos számítási eljárás?

A gyorsulást meghatározó formula segítségével egyedi következtetéseket vonhatunk le, a számítások segítségével állíthatjuk azt, hogy a kocsi egy adott időpontban egy meghatározott távolságra van a kiinduló ponttól. Előre kiszámíthatjuk, hogy miként fog viselkedni a rendszer egy adott súly esetén, amit megfogalmazhatunk igaz vagy hamis állítás formájában. Utána a kísérlet során méréssel ellenőrizhetjük, hogy amit jósoltunk, igaz-e. Van tehát egy mondatunk, ami igaz vagy hamis, és ez a mondat következménye egy formulának. Ekkor azonban a formula is jelentéssel kell, hogy bírjon, máskülönben nem következne belőle semmi. Tehát a példa megoldását nyújtó (10) formula nem csak hasznos segédeszköz, hanem igaz állítás.

Mi az, ami nem következik abból, hogy igaz állítások következnek a formulából? Nem következik belőle, hogy a formula azonos egy fizikai természettörvénnyel. A természetnek nincs saját nyelve, az ember az, aki beszél. A példa megoldását jelentő (10) formula nem maga a természettörvény, hanem egy modell, ami meghatározott határfeltételek között igaz, azon túl nem. Ezen kívül egy modellnek nem kell feltétlenül matematikainak lennie. Egy valóságos kocsi, és az azt mozgató súly viselkedése olyan módon is megjósolható, hogy mind a kocsit, mind a súlyt arányosan lekicsinyítjük, és ennek az arányosan kicsinyített modellnek határozzuk meg méréssel a gyorsulását, majd ennek alapján következtetünk arra, hogy mi fog történni a valóságban. 

Amikor hiszünk abban, hogy a gyorsulást meghatározó formulánk igaz, akkor abban hiszünk, hogy általánosan alkalmazható az alkalmazási feltételei között. Ez a következőket jelenti:

(i.§) Állandóság: meghatározott két tömeggel különböző időpontokban elvégezve a kísérletet mindig ugyanazt a gyorsulás értéket kapjuk. Vagyis föltételezzük a fizikai törvények állandóságát, hiszünk abban, hogy bármelyik jövőbeli időpontban is mérünk, ugyanazt az eredményt kapjuk, és abban is hiszünk, hogy ha korábban végeztük volna el a kísérletet, akkor korábban is ugyanazt a kísérleti eredményt kaptuk volna.

(ii.§) Interszubjektivitás: a kísérletet más is elvégezheti, mondhat közben bűvös szavakat, erősen gondolhat arra, hogy ne gyorsulva mozogjon a kocsi, hanem egyenletesen vagy lassulva, mindez hiába, az eredményt nem fogja befolyásolni.

(iii.§) Általánosság: abban is hiszünk, hogy a természet egységes, azaz a kísérleti rendszert számos más helyére is elszállíthatnánk a Földnek, a gyorsulás értéke, a kísérlet eredménye ugyanaz lenne.

(iv.§) Megismételhetőség: a kísérleti elrendezést más inercia rendszerben, hasonló eszközökkel fölépítve, más, de azonos tömegű kocsival, más, de azonos tömegű súlyokkal, más csigával és kötelekkel, az eredmény továbbra is változatlan lenne.

(A fenti négy pontban megfogalmazott kikötések alkalmasak a valóságos és nem valóságos fizikai jellemzők elválasztására.)

A példa, a kísérleti elrendezés megfogalmazható a kibernetika nyelvén is, amit más írásomban már említettem, és később is alkalmazni fogok. Kísérleti elrendezésünk megfelel egy automatának – fekete doboznak – melynek bemeneti jellemzői a kocsi és a súly tömege, kimeneti jellemzői, pedig a kocsi gyorsulása, pillanatnyi sebessége és helye.

2.ábra

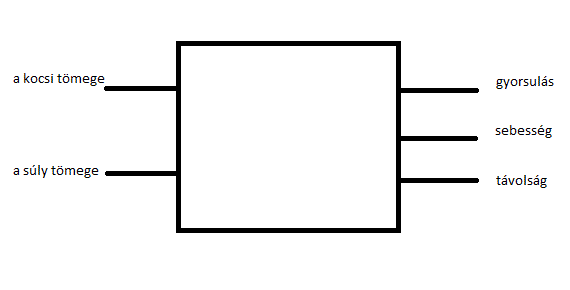
 Az automatának, mint egyedi absztrakt létezőnek (absztrakt partikulárénak) minden egyes kísérleti megvalósítása az absztrakt partikuláré egy instanciája. Ez semmi mást nem jelent, mint hogy a szónak egy később precizírozott értelmében, mindezek a megvalósítások egyformák abból a szempontból, hogy a kísérlet, a bemeneti értékek széles tartományán belül, minden esetben megegyező mérési eredményeket hoz létre.

Aktuális vagy potenciális értékek?

Milyen fajta létezők a formulák értékei szemantikai szempontból: aktuális értékek – egy adott tömeg, egy adott sebesség és gyorsulás, egy adott időpont – vagy potenciális értékek, másképp mondva lehetséges értékek, amelyeket a kísérleti elrendezéssel mérhetünk? A kérdés hasonlóképpen vonatkozik az automata modellre is, amikor egy fekete doboz kimeneteinek tekintjük a rendszer viselkedését különféle súlyok hatására. Milyen fajta létezők között ad meg összefüggést az automata, aktuális állapotok, vagy potenciális (lehetséges) állapotok között? A válasz mindkét esetben az utóbbi. Mind a fizikai formulák, mind az automata viselkedését leíró szabályok, lehetséges értékek közötti összefüggéseket adnak meg, írnak le. Ezek az összefüggések tartalmazzák a határfeltételek közötti összes lehetőséget, és így segítségükkel ki tudjuk számolni, meg tudjuk határozni, hogy ha a súly egy adott tömegű volna, akkor hogyan mozogna a kocsi. A potenciális értékekből akkor válik aktuális érték, amikor konkrét kísérletet végzünk, illetve amikor az automata meghatározott bemeneti jelet kap.

Lehetőség és szükségszerűség

Lehetséges-e, hogy a kocsi egy meghatározott ’a₁’ gyorsulással haladjon? Igen, ha tudunk olyan súlyt akasztani a kötél végére, ami éppen ezt a gyorsulást okozza. Mindez az automaták nyelvén azt jelenti, hogy lehetséges, hogy az automata egyik kimenete – a gyorsulás –­­­­ meghatározott értékű legyen, ha van olyan bemeneti értéke az automatának, amire az adott kimeneti állapot az automata válasza.

Szükségszerű-e, hogy a kocsi soha nem halad állandó sebességgel ebben a kísérleti elrendezésben? Igen szükségszerű, mert ez levezethető a formulából. Az automaták nyelvén ez azt jelenti, hogy bármely bemeneti hatásra érvényes lesz, hogy a sebességet jellemző kimenet soha nem konstans függvény.

Mindennek az a tanulsága, hogy a formula nem csak igaz, hanem szükségszerűen igaz, és a következtetést megalapozó szerepe jelenti a (10) formula szükségszerű igazságát. (Ezt a logikai szerepet a következő írásomban egy példával, egy automata modell segítségével pontosabban megfogalmazom.)

A példa létezési előfeltevései

Alkalmazzuk Quine létezés kritériumát, amit korábbi írásaimban több alkalommal tárgyaltam és értelmeztem a saját felfogásomban. Ekkor a fizikai jellemzőket függvényekként ábrázoló formális nyelv választása metafizikai döntést is magában foglal, azaz elköteleződést bizonyos fajta létezők mellett. Ebben a felfogásban az egyedi fizikai tárgyak mellett, mint amilyen a kocsi és a súly, ezek tömege és helye is létezik. Ez, a formulákat szó szerint értelmezve, valamiféle realista metafizikai álláspontot jelent, de összeegyeztethető ezzel ellentétes filozófiai álláspontokkal is, pl. a fikcionalizmussal. Utóbbi esetben azonban magyarázatra szorul, hogy mi a különbség a kopogó szellemekben való hit és a valós számok alkalmazásában való hit között?

Fizikai tárgyak

1. A példa értelmezhetetlen, ha nincsenek fizikai tárgyak, azon belül merev testek, nevezetesen az a merev test, amihez kötötten a példa inercia rendszerét elképzeljük. A fizikai tárgyakat, ezen belül a merev testeket értelmezhetjük komplex struktúraként, összetett létezőként, de odáig nem juthatunk el, hogy valójában azok nem is léteznek, mert nem atomiak. Ezzel kivágnánk magunk alatt a fát.
2. A példa értelmezhetetlen, ha nincsenek fizikai tárgyak, azon belül merev testek, nevezetesen a kocsi, a csiga és a súly.
3. Az időben egyre gyorsulva mozgó kocsi helye és sebessége is változik az időben. Vajon eközben azonos marad-e önmagával? Feltételezzük, hogy igen, különben a példa értelmetlen, mert nem tudjuk, miről beszélünk.

Idő

A kocsi gyorsulva mozog az időben, de vajon a mozgását leíró formula mennyit fejez ki az idő természetéből? Ha semmit, akkor a sebesség és gyorsulás fogalma is értelmezhetetlenné válik. Tehát hinnünk kell abban, hogy formulák valóságos időbeli összefüggéseket írnak le. De a formulák csak az időbeli viszonyokról, az idő B sorozatáról szólnak, nem említik, nem is használják a múlt, jelen vagy a jövő mindennapi léthez kötődő fogalmát. Az 1. ábra világosan mutatja, hogy a formulák az idő tériesített fogalmát használják. (Ez a szövegek statikus világában nem is lehet másképp.) A formulák által leírt helyzetek sorozata az események időtlen létezését ábrázolja. A formulák személete filozófiai szempontból eternalista. Az ezzel szemben álló prezentizmus álláspontja tagadja, hogy a formulák igazak, és az idő valós természetét írják le, mert nincsen a formulákban kitüntetett szerepe a jelennek. Csakhogy akkor megmagyarázhatatlan, hogy a formulák miért eredményeznek igaz ­­– jelenbeli tapasztalatokkal igazolható vagy cáfolható – következtéseket.  Ha a következtés helyes, és a jelenbeli következmény igaz, akkor a kiinduló eternalista szemléletű premisszák is igazak kell legyenek.

Univerzálék

Tegyük fel, hogy a súly tömege éppen 500 kg, amit így fejezhetünk ki:

(11) 500 kg = m(u)

Azt, hogy a tömeg állandó, nem változik az időpontok T tartományában, ilyen módon könnyen kifejezhető, ha a tömeget relációs jellemzőnek tekintjük:

(12) ∀t.t∈T→ 500 kg = m(u,t)

Azaz, az idő T tartományán belül a ’u’ jelű objektum tömege minden esetben 500 kg.

Csakhogy (12) –ből logikailag következik az alábbi formula:

(13) ∀t: t∈T→ ∃y. y = m(u,t)

 Azaz, a ’u’ jelű objektumnak a T idő tartományban mindig van tömege. Ez pedig már létezési állítás, annak az állítása, hogy létezik olyan mérési eredmény, mint az 500kg. Ez azt jelenti, hogy u-nak bármely tÎT időpontban van tömege.  Miféle ontológiai kategóriába tartozik a ’tömeg’, azaz a lehetséges mérési eredmények azon halmaza, melynek elemei a tömegek egyes értékei?

Vannak filozófusok, akik az ontológiailag sivár tájakat kedvelik, és ezért olyan nyelvet használnak, amelyik nem feltételezi a ’500 kg-osnak lenni’ tulajdonság létezésében való hitet. Ezek a filozófusok azt a tény, hogy a súly 500 kg-os, és ez nem változik T idő tartományon belül, egy R relációval fejezik ki ilyeténképpen:

 (14) ∀t. t∈T→ R(u,t) ahol R(u,t):= u 500 kg-os t időpontban

 Mi ennek a haszna filozófiai szempontból? Az, hogy nem kell feltételezzük a 500 kg-os lehetséges mérési eredmény – valójában egy tulajdonság – létezését, hanem csak egy halmazt, egy összességet, amelyben az összes 500 kg-os dolog benne van. Ebben a felfogásban 500 kg-osnak lenni annyi, mint egy halmaz elemének lenni.

Ez pl. Willard van Orman Quine vagy David Lewis felfogása. Két baj van ezzel. Az első, hogy amit nyerünk a réven, elveszítjük a vámon. Ezen a nyelven nem kell föltételezni az egyedi fizikai tárgyak mellett azok fizikai jellemzőinek a létezését, viszont jóval bonyolultabb – ha nem éppen lehetetlen – megfogalmazni a példa megoldását. A másodikat így fogalmazza meg Armstrong:[3] “…Azt mondani, hogy az elektronok azért elektronok, mert elemei az elektronok osztályának, kocsi húzza a lovat, típusú gondolkozás. Valójában azért elemi egy osztálynak, mert elektronok.” Formális nyelven kifejezve Armstrong gondolatát: xÎelektronok-halmaza:= xÎ{x: x-elektron}. Ugyanis a halmazba való tartozás nem kötődik szükségszerűen valamiféle tulajdonság kritériumhoz, bármiféle jól meghatározott dolgok, bármiféle önkényes, de egyértelmű összessége is egy halmaz. Ezért a halmazba való tartozás nem lehet magyarázó elv.

Trópusok

Csak a kocsi tömege létezik, vagy létezik maga a tömeg, mint univerzálé? A realizmus igenlő választ ad az utóbbira, mást az arisztotelészi, megint mást a platóni felfogás. A trópuselmélet köztes választ ad: létezik a kocsi tömege és létezik a súly tömege is, de ezek nem azonosak.[4] Fontos ezt jól megérteni. Szokásos fizikai megfogalmazásban, tegyük fel, hogy mind a kocsi, mind a súly 500kg tömegű. Korábbi formalizmusunkkal ez így írható föl:

500 kg = m(k) és 500 kg = m(u). De ebből az következik a logika szabályai szerint, hogy a kocsi tömege azonos a súly tömegével, azaz m(k) = m(u). A trópuselmélet szerint ez elfogadhatatlan, mert mindkét tömeg partikuláris létező, amelyik különbözik a másiktól. Legfeljebb azt mondhatjuk, hogy a kocsi tömege egyforma a súly tömegével, amit ekvivalencia relációval fejezhetünk ki formális nyelven: m(k) ≅ m(u). Az ekvivalencia osztályokat a tömegek azonos számértéke határozza meg. A trópuselmélet tehát ellentmond a fizika szokásos gondolkozásmódjának, a formulák szó szerinti értelmezésének.

További feltevések

1. A vonatkoztatási rendszer egy merev test, ahhoz rögzítetten képzeljük el a koordináta rendszert, amely alapján a testek mozgását leírjuk. A kísérleti elrendezés olyan elemei, mint a kocsi, csiga, és egyéb alkatrészek valóságos létezők, ezzel szemben a koordináta-rendszer a valóságban nem létezik, hasznos fikció csupán, melynek segítségével megadjuk a kocsi helyét. De bármennyire fikció a koordináta-rendszer, a segítségével meghatározott adat, pl. a kocsi mindenkori helye, tény, és nem fikció. Ez azért nem ellentmondás, mert a koordináta rendszer része a nyelvnek, a keretelméletnek, amelyen leírjuk a valóságot. Tehát a leírás eszköztárának része a koordináta-rendszer, azon belül létezik, de nem létezik a kocsi és csiga mellett, mint mérő rudak rendszere.
2. Feltételeztem, hogy a kocsinak annyiféle helye lehet, ahány valós szám van. Az időt is folytonosnak feltételeztem, sőt, valós számmal fejeztem ki a tömeget is. Igaz-e ez a feltevés? Nyilván nem. Nincs annyiféle fizikai jellemző,mind ahány valós szám van, mivel a fizikai jellemzők lehetséges mérési eredmények, és egy mérési eredmény mindig racionális szám, vagyis mindig valamilyen tűréssel és a hozzá tartozó valószínűséggel értendő. Célszerű egyszerűsítés annak feltételezése, hogy a kocsinak minden időpillanatban egyértelműen meghatározott helye és tömege van, melyet egy valós számmal fejezünk ki, de valójában mindig egy valószínűségi eloszlás tartozik a fizikai jellemzőkhöz. Az a feltételezés, hogy a mérések mögött van egy egyértelmű valós számmal rendelkező érték, és csak a mérés tulajdonsága a bizonytalanság forrása, egy lehetséges filozófiai álláspont, de tapasztalatilag nem igazolható.

Külső és belső kérdések

Értelmes külső kérdés, hogy mi köti össze a kocsit és a súlyt, vagy, hogy számolunk-e a kötél súlyával és megnyúlásával.[5] (Azért külső kérdés, mert az alkalmazott modellre, annak egyszerűsítő feltevéseire kívülről kérdez rá.) Értelmes külső állítás, hogy a kísérleti elrendezésben nem foglalkozunk sem a kocsi színével, sem azzal, hogy miközben mozog, a kerekei elfordulnak, és így a kocsi belső relációi – a kerék viszonyai a kocsiszekrény alkatrészeihez képest – megváltoznak.[6] Viszont zavarba ejtő állítás egy olyan metafizikai kijelentés, hogy „a kocsi tömege a ’tömeg’ fogalmának egy instanciája.” Tökéletesen értelmes belső állítás, hogy a kocsi t₁ időpontban s₁ helyen, t₂ időpontban egy ettől eltérő s₂ helyen van. Viszont nincsenek ehhez hasonló olyan események, mint például „A kocsi tömege instanciálódik a ’tömeg’ fogalmából.”, vagy „A kocsi sebessége instanciálódik a ’sebesség’ fogalmából”, holott a megfogalmazás könnyen félreérthető ilyen módon. Ez súlyos hiba, mivel egy külső állítást tévesen belső állításként kezel. A belső állítások igazságtartalma, a keretelmélet ismeretében tapasztalatilag ellenőrizhető, ezzel szemben a külső állítások nem függetlenek a választott keretelmélettől, a választott kísérleti elrendezéstől és az alkalmazott nyelvtől, nem önmagában a világról szólnak. A keretelmélet, a nyelv választása is egyfajta tény, de más szintű tény, mint amikor az elmélet és annak nyelve használatával belső állításokat teszünk. (Előző írásomban ezzel foglalkoztam.) A kettő összekeverése hibás filozófiai spekulációk forrása. Ilyen kérdésekhez vezet: mi köti a súly fogalmát a kocsihoz? A kapcsolatra, a kötésre vonatkozó kérdés értelmes a kocsi és a súly viszonyában, utalva a kötél használatára, de az alkalmazott kísérlet és keretelmélet fogalmi rendszere nem ilyen módon kapcsolja össze a kísérlet tárgyait.

A poszt szövege letölthető innen: http://ferenc.andrasek.hu/blog/kocsi-es-suly.pdf

 Jegyzetek

[1] A példát Walter Warwick Sawyer, Mi a matematikai analízis (What is Calculus About?), (1974) Gondolat, Bp. p.35. c. könyvéből vettem. A szerzőről: http://plus.maths.org/content/w-w-sawyer-passes-away

[2] Az analitikus és szintetikus igazságok megkülönböztetésével kapcsolatos vitában Grice és Strawson álláspontjával értek egyet, nem pedig Quine-val. Grice - Strawson, „In Defense of a Dogma.” (1956) The Philosophical Review, Vol.65, magyarul „Egy dogma védelmében” in.  Herbert Paul Grice: Tanulmányok a szavak életéről, (2011) Gondolat, Bp.

[3] „…to say that electrons are electrons because they are part of the class of electrons puts the cart before the horse. They are part of the class of electrons because they are electrons…” David Malet Armstrong (1989) Universals: an Opinionated Introduction. Boulder, Colorado: Westview Press. p. 37, 41.

[4] Ujvári Márta több tanulmányában és könyvében is foglalkozott a témával: Metafizikai dilemmák (2009) L’ Harmattan, Bp.

[5] A ’külső-belső’ fogalmi distinkciót Carnap terminológiájának szellemében használom.

[6] Súlyos filozófiai hiba, amit némelyik filozófus elkövet, amikor minden relációt külsőnek tekint.