1. Indexek és relációk

Nekem úgy tűnik sok filozófus óvatos távolságtartással kezeli a relációkat, és sokan bizonyos előítéletekkel közelítenek ehhez a kategóriához. A következőekben azt szeretném elmondani, hogy  én miért nem tartom szerencsésnek, ha indexekről beszélünk relációk helyett. Egyszerű példa segítségével fogom ezt elmagyarázni:

(1) Emma magasabb mint Péter.

(1.1) Formális nyelven: M(e,p)

Ez igaz volt sok évvel ezelőtt, amikor Emma négy, Péter két éves volt, de mikorra felnőttek, és Emma húsz, Péter tizennyolc éves lett, már megfordult az arány, és Péter volt magasabb Emmánál, tehát (1) mondat nem igaz.  A változó igazságértékek homályos világát elkerülhetjük két módon is: relációk vagy indexek használatával.

Ternáris (háromargumentumú) relációk használata

(2) Emma magasabb mint Péter t₁ időpontban és Emma nem magasabb mint Péter t₂ időpontban.

(2.1) M(e,p, t₁) & ~M(e,p, t₂)

Ugyanez a gondolat indexek használatával:

(3) Emma magasabb mint_t1 Péter és Emma nem magasabb mint_t2 Péter.

(3.1) M_t1(e,p) & ~M_t2(e,p)

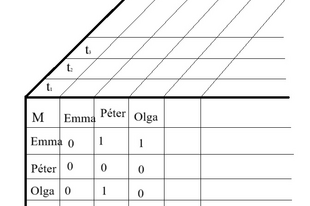
A ternáris relációkat három dimenzióban célszerű ábrázolni:

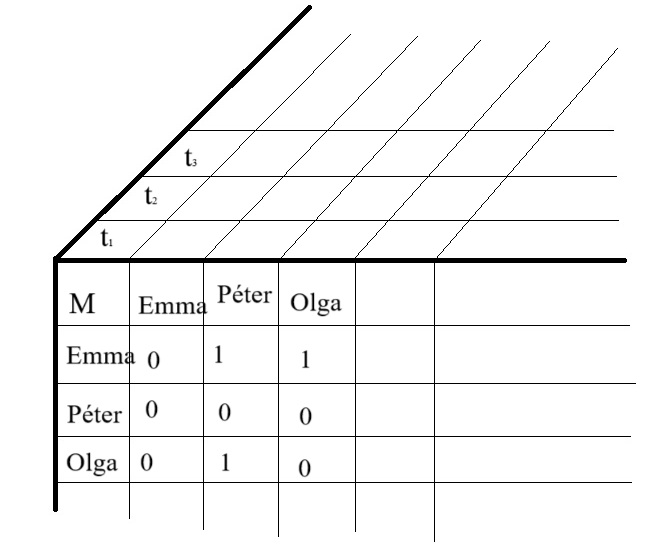
Az indexek megelégszenek két dimenzióval, ez kétségtelenül előnyük.

A második táblázat azt is ábrázolja, hogy t₂-kor Olga és Péter egyforma magasak voltak.

Figyeljünk föl arra, hogy a „t₁” és „t₂” jelek, melyekkel két különböző időpontot jelölök, szintén indexeket használnak. Ennek didaktikai okai vannak. Nevezhetnénk a két különböző időpontot „a”-val és „b”-vel, de ekkor a jelölés nem sejtetné, hogy mindkét jel egyazon kategórián belüli dologra, az időre utal, és azon kívül, a „t” jel, az angol time=idő szóra asszociál, a könnyebb megértést segítendő. A fő probléma a következő. Relációk használatával könnyen kifejezhető, hogy

(4) Valamikor Emma magasabb volt mint Péter, de sok évvel később már Emma nem magasabb Péternél.

(4.1)   $x$y (M(e,p,x) & ~M(e,p,y)) & y későbbi mint x

Jelen esetben „valamikor”=t₁, a „sok évvel később”=t₂. Ugyanez indexek használatával nem fejezhető ki korrekt módon. Legalábbis furcsa lenne az alábbi megoldás:

(4.2) $x$y M_tx(e,p) & ~M_ty(e,p) & y későbbi mint x

Példánk esetén az indexek használata a háromargumentumú relációk metszeteit jelenti, amint az  1. ábra mutatja.

2. Külső és belső relációk

Most térjünk rá egy másik makacs előítéletre, miszerint minden reláció külső tulajdonság. Kezdjük azzal, hogy nem minden egyargumentumú predikátum, azaz nem minden tulajdonság belső. Mondjuk Richard Wagner Parsifal című operájának számos jellegzetessége, tulajdonsága van, de az bizonyára nem tulajdonsága, hogy Emma kedveli, Anna pedig nem kedveli ezt az operát. Ugyanakkor a hangok magasságának és időtartamának egymáshoz való viszonya nyilvánvalóan belső tulajdonsága a zenének, így ennek az operának is. Az emberi testnek belső tulajdonsága hogy a szív a középvonaltól kissé balra helyezkedik el, és ezért a tüdő bal oldali része kisebb mint a jobb oldali. A gépeknek belső tulajdonsága, hogy melyik fogaskerék melyik másikhoz kapcsolódik, vagy a digitális hangnak, hogy a mintavételi frekvencia magasabb, mint a legmagasabb hallható hang. Valójában a tárgyak tulajdonságait meghatározó szerkezeti tulajdonságok, mind-mind relációkat jelentenek, azzal írhatóak le.

Hogy egy tulajdonság mitől belső és mitől külső, azt nem könnyű megválaszolni, hasonlóan ahhoz a kérdéshez, hogy mi a különbség a szükségszerű és a lényegi tulajdonságok között. Ez utóbbi kérdésekre most nem térhetek ki. Csak annyit szeretnék megjegyezni, hogy ezek közül egyik fogalmat sem tekintem spekulatívnak, üresnek vagy álfogalomnak.

Innen letölthető: https://ferenc.andrasek.hu/blog/111-indexek-és-relációk.docx