A következőkben megmutatom, hogy egy inercia rendszerben egy tömegpont mozgása felső határsebességének létezése mellett logikai érvek is szólnak, ha a tér és idő atomos szerkezetű. Az érv alapötletét Zénón jól ismert aporiái sugallták.[i]

 Tegyük fel, hogy ’m’ tömegpont egyenes vonal mentén halad A pontból B pontba, t₁ időpontban indulva és t₂ időpontban megérkezve. A következő feltevéseink vannak:

 (1) Feltesszük, hogy a megtett út és a hozzá tartozó idő is diszkrét és nem folytonos, ami semmi mást nem jelent, mint hogy a tér és idő atomokon adott egy az egész számok nagyság szerinti rendezésével izomorf rendezés. Ezért mind a tér, mind az idő koordinátát egész számok sorozatával ábrázoljuk. Ebből következik (1.1) és (1.2) feltevés:

 (1.1) A és B pont között csak véges sok pont található, melyek mindegyikéhez egyértelműen meghatározott az előző és a következő pont. Tetszőleges x pont esetén x+1 a következő és x-1 a megelőző pont.

 (1.2) Az útvonal pontjai – melyeken az m tömegpont áthalad – sorba rendezettek olyan módon, hogy bármely két különböző pont közül el tudjuk dönteni, hogy melyik van közelebb a végponthoz, B-hez.

 (2) A pont minden időpontban van valahol, azaz minden időpontban van helye, és ez a hely a vonal egy pontja.

 (3) Ha a pont valahol tartózkodik, akkor ahhoz tartozik egy időpont.

 (4) A pont bármely pontból csak a következő vagy az előző pontba mozdulhat el. A helyeket, melyekhez a pont a következő időpontban elmozdulhat, szomszédos helyeknek fogom nevezni. A „szomszédos hely” fogalma két vagy többdimenziós diszkrét térben is értelmezhető, melyekre a későbbiekben kitérek.

 (5) Jelen mozgás esetén a pont soha nem halad visszafelé, ezért az ’m’ pont mozgása során minden helyet érint A és B között, egyet sem hagy ki vagy ugrik át.

 A következő feltevés csak egy determinisztikus világban érvényes:

(6) A pont minden időpontban egy és csak egy helyen van, a hely determinisztikus jellemző. Más felfogásban elképzelhető ezzel szemben az is, hogy a pont helye csak mint valószínűség értelmezett, azaz a pont helye egy statisztikus eloszlás függvény.

 Tegyük fel  a következőt is:

 (7) A pont folyamatosan halad előre, tehát ha x időpont későbbi mint y, akkor a pont x-hez tartozó helye közelebb van B-hez, mint a korábbi y időpontban lévő helye.  Ebből az következik, hogy miközben halad a pont folyamatosan mozog bármely t₁ és t₂ közé eső tartományban – t₁-t és t₂-t is beleértve. A folyamatos mozgás közben amennyiben két időpont nem azonos, akkor a pont hozzá tartozó két helye is különbözik.

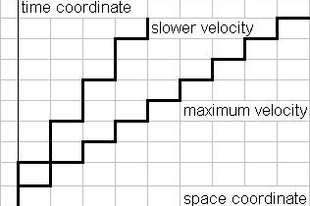
 A korábbiak alapján belátható, hogy csak egyetlen sebességgel haladhat a pont, és az éppen a legrövidebb hossz és időtartam által meghatározott maximális sebesség.  Tegyük fel ugyanis, hogy egy időatom alatt a pont kettő vagy több tératomot halad előre. Mivel feltételeztük, hogy a pont nem hagy ki helyet és mindig van valahol, diszkrét időskála alapján nem tudhatjuk, hogy hol van a pont, ha egyszerre több tératomot halad egy időatom alatt. Valahol lennie kell, de feltételeztük, hogy egyszerre több helyen nem lehet. Ez viszont ellentmond annak, hogy egy időatom alatt több tératomot halad. Amennyiben viszont a pont lassabban halad mint a maximális sebesség, akkor némelyik két szomszédos időponthoz egyazon hely tartozik, ami viszont a folyamatos haladás kikötését sérti meg. Ha a folyamatos haladást elvetjük, akkor a lassabb sebességeknek a pont szaggatott előrehaladása, majd a sebességtől függően hosszabb-rövidebb ideig való egy helyben maradása fog megfelelni. Ekkor a pont ilyen sajátos szaggatott módon a maximális sebességnél lassabban is haladhat. (Lásd az 1. ábrát.)

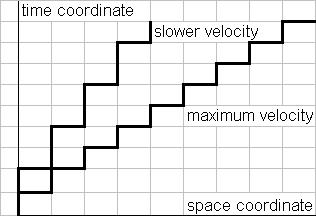
1. 1. Figure

Ez a szaggatott jellegű haladás különös, de nem ellentmondásos, ugyanakkor az atomos szerkezetű tér-idő számos további kérdést vet föl.

 A fenti ábrán szabályos egyenes vonallal ábrázoltam a koordinátákat. Ha azonban a távolság valóban diszkrét atomokból áll, akkor semmi sem támasztja alá a diszkrét tératomok szabályos elhelyezkedését. Egyedül az (1) feltétel szabja meg a diszkrét tératomok logikáját, minden más előítélet. Egy folytonos világból szemlélve hullámvonalon is elhelyezkedhetnek a diszkrét világ tératomjai, nem csak egyenes vonalban. Ebből következik, hogy az egydimenziós tér-időt ábrázoló négyzetháló sem kell feltétlen szabályos geometriai alakzat legyen egy folytonos világból nézve. Ha egy gumilapra rajzoljuk az egydimenziós tér-idő négyzethálóját, a gumilapot nyújthatjuk, zsugoríthatjuk, akkor is megfelel a logikai követelményeknek. Mi ezen logikai követelmények lényege? Az, hogy nem lehet átugorni rácspontokat a téridőben.[ii] Ezért rajzoltam lépcsőgrafikont a maximális sebességhez is és nem egyszerűen egy vonalat.

 Jobban érthető ennek a jelentősége ha kétdimenziós térben gondolkozunk.

Miért gondoljuk, hogy a két pont közötti távolságot egy egyenes és nem egy görbe vonal ábrázolja? Azért mert úgy véljük a távolság a legrövidebb út a két pont között, és az egyenesnek megfelelő kötéldarab rövidebb mint a görbe vonalnak megfelelő kötél. Az egyszerűség kedvéért maradjunk a szabályos elrendezéseknél. Legyen egy kétdimenziós diszkrét világnak adott tizenkét atomi helye az alábbi elrendezésben:

2. 2. Figure

Milyen messze van A és K? Attól függ miképpen haladhatunk. A (3) pontban egydimenziós térben rögzítettem, hogy a mozgás egymást követő diszkrét időpontokban mindig csak a szomszédos helyre történhet. Egydimenziós térben a szomszédos hely fogalma kézenfekvő volt, viszont két vagy többdimenziós térben már nem az, többféle lehetőség között választhatunk. Ha haladhatunk ferdén, akkor F-et érintve A és K között két atom távolság a legrövidebb út. Ha csak jobbra - balra, föl és le haladhatunk, akkor viszont a távolság négy tératom.

 Milyen messze van egymástól A és D pont? Intuíciónk azt súgja, hogy három atom távolságra. Vajon ez a legrövidebb távolság A és D között? A válasz most is attól függ minként szabad haladni. Ha szabad bármely irányban haladni a rácspontok között, akkor D-t összeköthetjük E-vel. Az E pont mellett van A pont, és így csak két atomnyi távolságra van A és D. Ha két pont közötti legrövidebb út a távolság, és ezt az utat nem tiltja meg semmi, akkor el kell fogadjuk, hogy az A és D közötti távolság kettő. Ez azonban ellentmond annak a korábbi kikötésnek, hogy nem lehet átugorni, kikerülni tér atomokat. Az imént viszont épp ezt tettük, ezért ezt a lehetőséget kizárjuk, így az A és D közötti távolság három. Továbbra is nyitva marad a kérdés, hogy megengedhető-e a mozgás pl. A-ból F-be, haladhatunk-e ferdén? (Hasonló kérdés tehető föl három dimenziós térben is.) Ugyanis F-en áthaladva is három tér atomot kell haladjunk A-ból D-be.

Fontoljuk meg milyen messze van A és L? A ferde haladást megengedve, de az ugrást megtiltva A és L között három különböző három atomnyi távolság van: A-B-G-L, A-F-K-L, A-F-G-L. Nem egyértelmű tehát a két pontot összekötő egyenes fogalma. Ha kikötjük, hogy csak jobbra-balra vagy föl-le változhat meg a pont helye egy időatom alatt – tehát nincs mozgás ferdén – akkor is megmarad az egyenes fogalmának többértelműsége, de így az A – L közötti legrövidebb távolság öt atom lesz. Viszont a Pitagorasz tétel semelyik esetben sem érvényes, és ezen az sem segít, ha nagyon sok pontra osztjuk a távolságokat.[iii]

 Jó lenne ezeket a furcsaságokat elkerülni egy folytonos tér-időhöz hasonló térben. Egy folytonos tér-idő modellnek talán megfeleltethető egy valószínűségi atomos modell, ahol a véletlenben lévő információ pótolja a folytonos mennyiségekben (a valós számokban) lévő információ többletet.

 Innen letölthető: http://ferenc.andrasek.hu/pdf-papers/time/zrel_hun.pdf

[i] Gondolatmenetem első verziója egy vitacikk részeként megjelent a Fizikai Szemle 2005/9 számában. Zénón aporiáiról Ruzsa Imre, A matematika néhány filozófiai problémájáról, (Tankönyvkiadó, Budapest, 1966, 65-66 o.) c. könyvében olvastam, innen jött az ötlet.

[ii] A rácspontokra vonatkozó megfontolást Bíró Tamás Sándor egy 2006-os a Szkeptikus konferencián elhangzott előadásából vettem.

[iii] v.ö.: Kris McDaniel: Distance and Discrete Space. Synthese (2007) 155: 157-162