Plantinga modális istenérve

A népszerű Kálvinista apologetika portál folyatta érdekes sorozatát, most éppen Plantinga modális istenérvét mutatta be, nagyon jól követhető előadásban. Plantinga modális istenérve a video előadásban így festett:

(1) Lehetséges, hogy Isten létezik.

(2) Ha lehetséges, hogy Isten létezik, akkor Isten létezik néhány lehetséges világban.

(3) Ha Isten létezik néhány lehetséges világban, akkor Isten létezik minden lehetséges világban.

(4) Ha Isten létezik minden lehetséges világban, akkor Isten létezik a valós világban is.

(5) Ha Isten létezik a valós világban, akkor Isten létezik.

A video későbbi megfogalmazásai a gondolatmenetet még finomítják, bevezeti a maximális kiválóságú és a maximális nagyságú lény fogalmát. Plantinga lényegesnek tartja ezt a fogalmi kettősséget, én viszont úgy gondolom, a két fogalom egyesíthető. Egy feltételezett ideális lény – pl. Isten – minden lehetséges világban maximális kiválóságú, ezt csökkentő, negatív tulajdonsággal nem rendelkezik, és ez miden lehetséges világban így van. A lehetséges kiválóságot úgy definiálja, hogy az eleve Isten fogalmának felel meg.  Nekem úgy tűnik, hogy az érv ezzel elköveti a petitio principii logikai hibát, eleve feltételezi a bizonyítandót. Ugyan miért kéne csak a maximális kiváló tulajdonságok létezését feltételezni? Teljesen jogos annak az ellenkezőjét szintúgy feltételezni, tehát hihetünk a maximális rosszaságú lény létezésében is, amelyik szintúgy maximális nagyságú, azaz minden lehetséges világban létezik. (Vannak, voltak ilyen vallások is.) Azon felül miért kéne csak a maximális kiváló tulajdonságú személy létezését feltételezni, miért ne feltételeznénk maximális kiválóságú fizikai tárgyak pl. a tökéletes sziget, vagy a tökéletes futó cipő létezését? Ennek azonban nincsen jelentősége, látni fogjuk, hogy az érv ettől még működik.

 A logika formulákkal dolgozik, tételei jelentés nélküli formulák. A levezetések során csak és kizárólag a levezetési szabályokra szabad hivatkozni, a formulák szándékolt interpretációjára nem. Ha mégis szükségünk van erre, akkor külön jelentés posztulátumot kell a bizonyításhoz fűzni. A bizonyítások tetszőleges szabatos interpretációja megengedett, ebben áll a logika általánossága. (Ezt sejtette meg Gaunilo a középkorban.) A fenti bizonyítás szigorúan véve nem logikai levezetés – bár így érthetőbb – hiszen nem tartalmaz formulákat, nem látjuk, hogy melyik sor milyen szabály alapján, miből következik. De megkísérelhetjük formalizálni. Megmutatom egy lehetséges formalizálását az én felfogásomban. A szokásos jelölést alkalmazom:

M:=lehetséges

N:=szükségszerű[i]

∃:=van olyan

A G tulajdonság (egyargumentumú predikátum) különleges létezőkre igaz. Nem tudjuk, hogy vannak-e ilyen létezők, azt sem hogy hányan vannak, de ha valamilyen x létező G tulajdonságú, akkor szükségszerűen G tulajdonságú. Másképp fogalmazva, ha van olyan w világ, melyben van olyan x, hogy x-G akkor minden w világban van olyan y, hogy y-G.

(1) M∃x Gx → N∃x Gx feltevés, a korábbiak tömör megfogalmazása

Első interpretáció: Gx := x – isteni lény

Ha isteni lény létezik néhány lehetséges világban, akkor isteni lény létezik minden lehetséges világban. Másképp ezt így mondhatjuk: ha lehetséges, hogy létezik isteni lény, akkor szükségszerű, hogy létezik isteni lény.

Második interpretáció: Gx:=x-tökéletes sziget

Ha tökéletes sziget létezik néhány lehetséges világban, akkor tökéletes sziget létezik minden lehetséges világban. (Máskülönben nem lenne tökéletes sziget.) Másképp ezt így mondhatjuk: ha lehetséges, hogy létezik tökéletes sziget, akkor szükségszerű, hogy létezik tökéletes sziget.

(2) M∃x Gx feltevés

Első interpretáció:

Lehetséges, hogy Isten létezik – pontosabban isteni lény létezik, de ezen most emelkedjünk felül.

Második interpretáció:

Lehetséges, hogy tökéletes sziget létezik.

(3) N∃x Gx (1)(2) következmény modus ponens alapján

(4) ∃x Gx (3) modális axióma alapján

(5)Tehát modális logikai igazság, hogy ha (M∃x Gx és (M∃x Gx → N∃x Gx)) akkor ∃x Gx.

Szavakban, első interpretáció: Feltevésünk szerint Isten olyan lény, amelyik ha lehetséges, hogy létezik, akkor szükségszerűen létezik (mert ilyen a természete). Másképp fogalmazva: Isten olyan lény, amelyik ha egyáltalán létezik egy lehetséges világban, akkor minden lehetséges világban létezik. Ezért, ha lehetséges, hogy Isten létezik, és érvényes az előbbi feltevésünk, akkor Isten szükségszerűen létezik, amiből az következik, hogy Isten létezik.

Szavakban, második interpretáció: Feltevésünk szerint A tökéletes sziget olyan dolog, amelyik ha lehetséges, hogy létezik, akkor szükségszerűen létezik (mert ilyen a természete). Másképp fogalmazva: A tökéletes sziget olyan dolog, amelyik ha egyáltalán létezik egy lehetséges világban, akkor minden lehetséges világban létezik. Ezért, ha lehetséges, hogy A tökéletes sziget létezik, és érvényes az előbbi feltevésünk, akkor A tökéletes sziget szükségszerűen létezik, amiből az következik, hogy A tökéletes sziget létezik.

(Óvatosságból nem bizonyítom be a tökéletes gonoszság létezését, bár ott bújik a lehetősége.)

Ez az érv érvényes (a premisszákból logikailag következik a konklúzió, függetlenül attól, hogy a premisszák – a kiinduló feltevések – önmagukban igazak vagy sem), azonban különbözik az ontológiai istenérvtől. (Nem láttam be azonnal, hogy az érv érvényes, később azonban rájöttem, hogy a lényege könnyen formalizálható, és ezért megváltoztattam a véleményem.) Figyeljünk meg, hogy megváltozik a helyzet, ha nem lehetőséggel, hanem kontingenciával számolunk. Kontingencia: lehetséges, hogy egy mondat (gondolat) igaz, de az is lehetséges, hogy nem igaz.

(1)  M∃x Gx → N∃x Gx  feltevés

Ha lehetséges, hogy Isten létezik, akkor létezése szükségszerű.

(2)  M∃x Gx és M~∃x Gx feltevés

Isten lehet, hogy van, lehet, hogy nincs.

(3)  N∃x Gx (1)(2)

(4) ~M~∃x Gx (3)

(5) M~∃x Gx (2)

(6) M~∃x Gx és ~M~∃x Gx (4)(5) ami ellentmondás

Lehetséges, hogy Isten nem létezik és nem lehetséges, hogy Isten nem létezik.

Beláttuk tehát, hogy ha föltételezzük, hogy Istennek a szükségszerű létezés a természete, és úgy véljük, hogy Isten lehet, hogy van és lehet, hogy nincs, akkor ellenmondásba keveredünk.

Korábban bebizonyítottunk egy tételt: (5) (M∃x Gx és (M∃x Gx → N∃x Gx)) → ∃x Gx

Minek a létezését bizonyítja ez a tétel a logikán kívüli világban? Egyáltalán minek vagy miknek a létezését bizonyítja? Némelyek szerint a levezetés bizonyítja egy logikán kívüli, nem absztrakt matematikai létező létét, nevezetesen Isten létét. Szerintem viszont egy logikai tételt bizonyítottunk be, egy modális logikai igazság létezését. Ennek a modális logikai tételnek számos interpretációja adható, a tökéletes szigettől, a tökéletes cipőig.[ii]

A logika formulákkal dolgozik, és levezetéseivel bizonyít logikai tételeket, ahol a premissza és a konklúziót összekapcsolva un. tautológiát kapunk. Ha a logikát kiegészítjük némi halmazelmélettel, akkor megkísérelhetjük fölépíteni a halmazelméletet és a struktúrák elméletét, melyekkel modellálhatjuk az aritmetikát, sőt, azon felül a többi számkört is. Így azt is igazolhatjuk, hogy 1+1=2. Da vajon igazolhatja-e bármilyen logikai levezetés logikán kívüli dolgok (pl. istenek vagy ördögök) létét?

A portál előadója Kalám vagy Leibniz istenérvével kapcsolatban korábban kizárta, hogy a világ létezését megalapozhatja egy absztrakt matematikai létező. Ez érvélésének sarokpontja volt. (A természeti törvényeket kihagyta a számításból.) Ugyanakkor mit tesz most, amikor úgy véli, hasznára válik ennek az ellenkezője? Ugyanis úgy tűnik, Plantinga modális logikai argumentuma logikai érvek alapján akarja alátámasztani logikán kívüli dolgok létezését. Pontosan azt teszi, amit a Kalám érv esetén kizárt. Itt azonban elfogadja. Én ebben következetlenséget látok. Spongyát rá, lépjünk tovább.[iii]

Buridán istenérve

A maga korában nagyhatású középkori francia filozófustól, Buridántól (Jean /John/. Buridan 1300-1358) származik a következő rejtvény, melynek lényege a következő. (Az érv Klima Gyula fordításában a jegyzetben olvasható.[iv])

(p)  Isten létezik.

(q)  Sem (p) sem (q) mondat nem igaz.

 Mit gondoljunk ennek a két mondatnak az igazságáról? Vajon melyik igaz közülük?

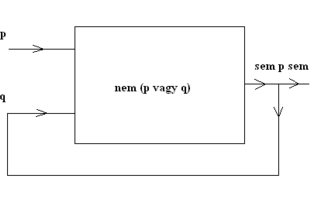
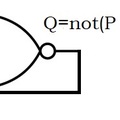
A (q) mondat ’vagy-nem’ kapcsolatot állít, mivel a „nem p és nem q” ekvivalens a „nem (p vagy q)” logikai struktúrával. A vagy-kapcsolat egyik összetevője egy létezési állítás, a másik összetevője pedig a vagy-kapcsolat önmaga. Különös mondat ez, mert igazságértéke – ha egyáltalán van neki – önmagától is függ. Ezért biztosan nem fordítható le a szokásos logikai keretek között. A 'vagy' kapcsolat előbbi tagját képviselje ’p’, az utóbit pedig ’q’ formula. Tehát p=:Isten létezik, q=:Sem az első, sem a második mondat nem igaz. Tehát ’p’ igaz, ha Isten létezik, hamis más esetben, és ’q’ igaz ha sem p sem q nem igaz. Szemléletesen ezt úgy fejezhetjük ki, hogy |q|=|nem(p vagy q)|, ahol az azonosság két oldalán formulák igazságértékei (faktuális értékei) szerepelnek. Az alábbi elektronikai modell fejezi ki p és q mondat logikai kapcsolatát.

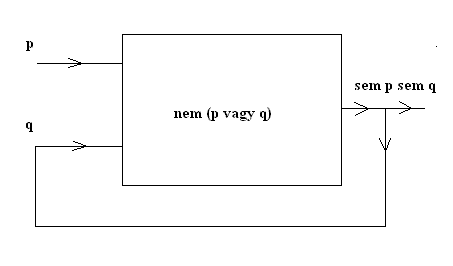
Visszacsatolással modelláltam q igazságértékének önmagától való függését. A p bemenet magas szintű, ha Isten létezik, alacsony szintű, ha nem létezik, a q bemenetre pedig az automata kimeneti állapota kerül vissza. A kimenetnek felel meg a „sem egyik sem másik nem igaz“ mondat. Tehát az automata kimenete akkor magas szintű, Isten nem létezik és mindkét mondat hamis, más esetben – pl. ha létezik Isten – az automata kimenete alacsony szintű. A vagy-nem igazságfüggvénynek a ’(p+1)*(q+1)’ az aritmetikai fordítása. (igaz=páratlan szám, hamis=páros szám) Ekkor a visszacsatolást kifejezhetjük egy matematikai (egyenlettel) formulával. Legyen „x ≅ y” kifejezés annak a jele, hogy mod(x,2) = mod(y,2), azaz vagy mindkettő szám páros, vagy mindkettő páratlan. Ekkor az aritmetikai modell alapján lefordítva Buridan istenérvét az alábbi aritmetikai állítást (egyenletet) kapjuk: q≅ (p+1)*(q+1). Ennek csak akkor van megoldása, ha p páratlan, de q páros. Visszafordítva ezt az eredményt a logika nyelvére azt kapjuk, hogy (p) igaz, viszont (q) hamis kell legyen, máskülönben ellentmondásba keveredünk. Tehát az érv szerint Isten létezik, máskülönben ellentmondásba keveredünk. Pontosan ez derül ki az elektronikus modell kipróbálásával is. Ha p alacsony szintű, akkor nem kapunk stabil kimeneti jelet, a kimenet felváltva hol magas, hol alacsony szintű.

Az elektronikus modellben a BurdianObj. és a BurdianMeta. munkalapok tartalmazzák a megfelelő automata modellt. Utóbbiban ábrázoltam egy véges világot. Ebben a világban három jellemző van: az első minden időben állandó y1=10 értéke fejezi ki Isten létét, a második y2=TRUE ha a (3) nevű mondat igaz, és y3=1 ha esik a hó. Ha tagadjuk Isten létét, amit úgy fejezhetünk ki ebben a modellben, hogy t₁,t₂,t₃,t₄ időpontok valamelyikében y1 értéke nem 10, akkor y2 jellemzőnek, (3) mondat igazságértékének nincs időben állandó értéke, miközben múlik az idő F9 gomb lenyomására.

(A modell táblázatkezelő formában innen tölthető le.)

Utóhang

Nekem – kívülállóként – úgy tűnik, a logikai istenérvek még a teológusok között sem népszerűek, csak egy kisebbség fogadja el. Pl.: a magyar katolikus lexikon írja:

„Ha Isten lényét közvetlenül föl tudnánk fogni, léte szükségszerűen adva volna részünkre. A földi életben azonban ez lehetetlen, így számunkra a tétel sem nyilvánvaló, hanem Isten léte bizonyítást igényel (STh I, 2, 2.; Gent. I, 12). A bizonyítás kizárólag a posteriori lehet: az okozatról az okra való következtetés (→a priori). Kiindulási alap a tapasztalat, melyből az →okság elvének metafizikai (egyetemes és szükségképpeni) érvénye juttat el bennünket a világ transzcendens okának ismeretéhez.”

A szöveg innen letölthető:

http://ferenc.andrasek.hu/blog/pdf/plantinga4.pdf

http://ferenc.andrasek.hu/blog/doc/plantinga4.docx

[i] A modális logikában nem rögzítik a modális operátorok (lehetséges, szükségszerű) jelentését. Az un. alethikus modalitásoknak is többféle értelmezése van: 1. lehetséges mindaz, ami nem logikai ellentmondás; 2. lehetséges mindaz, amit a természettörvények nem zárnak ki; 3. lehetséges mindaz, ami valamilyen kiinduló feltételek esetén levezethető természettörvényekből (nekem ez a felfogás szimpatikus). De másfajta modalitások is használatosak. Temporális modalitás: mindig p, néha p; deontikus modalitás: kötelező, hogy p, megengedett, hogy p; episztemikus modalitás: biztos, hogy p, nincs tudomásom róla, hogy nem p.

[ii] Egyszerű példa modális logikai levezetésre:

(1)Np ↔ ~M~p     

(2) p→Mp

(3) p→~N~p  (1)(2) kijelentés kalkulus

(4) N~p→~p (3) kijelentés kalkulus

(5) Nq→q (4) behelyettesítés q=~p

(5) egy interpretációja: ha szükségszerű, hogy a piszkavas nem tud egy pillanat alatt lehűlni, akkor a piszkavas nem tud egy pillanat alatt lehűlni (most sem).

Sok fajta modális logikai rendszer van, ezek különböznek az axiómáikban illetve a hozzá tartozó szemantikai interpretációban. Plantinga az un. S5 modális rendszerben gondolkozik.

Lényeges az is, hogy ebben a most említett felfogásban a szükségszerűséget és lehetőséget nem metanyelvi predikátumként, hanem operátorként értelmezzük. Ezért megengedettek a kevert használatok, pl. szükségszerű, hogy szükségszerű, hogy a háromszögnek három oldala van. vagy pl. lehetséges, hogy szükségszerű, hogy van maximális határsebesség. És semmi nem tiltja meg a modális logikában az ennél is bonyolultabb konstrukciókat. Amennyiben metanyelvi predikátumként értelmezzük a lehetőséget és szükségszerűséget, akkor az ilyen kevert használatok gondot okoznak. Jóval komplikáltabb a helyzet, amikor a modális operátorok kvantorokkal és predikátumokkal kevert formulákban jelennek meg. Az ilyen formulák szemantikai értelmezése már jelentős halmazelméleti ismereteket feltételez. Érdemes elolvasni a témáról Ruzsa Imre valamelyik könyvét, amelyik filozófiai elfogultságok nélkül, tudományos alapossággal tárgyalja a témát. (Természetesen számos angol nyelvű, vagy más idegen nyelvű ismertetése is van a tárgykörnek.) Ezek számos vitatott kérdést vetnek föl, melyekkel korábbi posztjaimban már foglalkoztam.

[iii] Egyéb internetes források:
https://study.com/academy/lesson/platingas-modal-ontological-argument-for-god.html

https://plato.stanford.edu/entries/ontological-arguments/

[iv]"Twelfth sophism: GOD EXISTS AND SOME CONJUNCTION IS FALSE

The twelfth sophism is 'God exists and some conjunction is false'. Let us posit that this is written on the wall and that there exists no other proposition than it and its parts. And then it is asked whether it is true or false.

We argue as before: for if it is true, then it follows that it is false; and if it is false, it seems to follow that it is true, for things are as it signifies, since its contradictory is false, namely this: 'God does not exist or no conjunction is false'. Solution: we should say that it is false, and the argument is solved as before. For although things are as it signifies according to its formal signification, yet, things are not as would be signified by the consequent implied by it and the case, and, assuming it to be named by the proper name A, its contradictory would be this: 'No God exists or no conjunction is false or A is not true'.

Similar sophisms could be formed concerning disjunctive propositions, as 'A man is a donkey or some disjunctive is false', positing that there is no other disjunctive; and the same goes for exceptive [propositions], as for example, 'Every proposition other than an exceptive is true', positing that there are no propositions except this exceptive and two others, namely, that God exists and that a man is an animal; and thus also with exclusives, as when Socrates says: 'God exists' and Plato says: 'Only Socrates says something true', and nobody says anything else. Other sophisms can also be formed about the fact that it is possible for a proposition to be doubtful or not doubtful, known, or not known, believed or not believed." John Buridan, Summulae de Dialectica (Summulae), an annotated translation with a philosophical introduction by Gyula Klima, New Haven: Yale University Press, 2001, Sophismata, c. 8, p. 980.