Bevezetés

Richard Wagner Parsifal c. operájában Gurnemanz mondja az akkor még balgatag Parsifalnak: „Fiam, ez itt a térré vált idő. (Míg Gurnemanz és Parsifal halad, a szín változik. Belépnek Grál várának hatalmas termébe.)”[i] Az öreg, bölcs lovag ’idő’-n nyilván a szent időt, a bibliai időket értette, Jézus történetére gondolt, nem pedig az ’idő’-re általában, és a ’tér’ amit említ, az sem a puszta fizikai tér, hanem a vár szent tere. De ez minket most nem érdekel, mi a két fogalom viszonyát a maga általánosságában fogjuk megvizsgálni. Filozófiával foglalkozunk és nem teológiával.

Egyszerű példa segítségével magyarázom el, hogy mi érdekli a fizikust, és mi a filozófust az idővel kapcsolatban. A válasz röviden a következő: a fizikust az ’egyidejűség’ fogalma érdekli míg a filozófust a ’jelen’ fogalma. A két fogalom között számos kapcsolat, hasonlóság van, de ugyanakkor lényegesek az eltérések is. Lássuk a példát.

Az idő problémája a fizikában és a filozófiában

Távol az űrben A űrhajóban utazunk. Mivel űrhajónk jókora távolságra van minden égitesttől, és nem gyorsul, hanem egyenletesen halad, föltételezzük, hogy űrhajónk inercia rendszer. Ez azt jelenti, hogy űrhajónkon belül jó közelítéssel érvényesek a klasszikus fizika törvényei. Ez kísérletekkel ellenőrizhető. Barátunk N.N. úr mellettünk egy irányban, azonos sebességgel halad a B űrhajóban. Ekkor az ő rendszere is inercia rendszer. Mindkét űrhajóban vannak pontos, jól működő fizikai mérőeszközök, és azt tapasztaljuk, mindkét űrhajóban érvényes a klasszikus fizika ’F = m×a’ törvénye. (A tömeg skalár, az erő és a gyorsulás vektor mennyiségek erre utal a kövér betűk használata.) Mindkét űrhajóban van egy-egy pontos óra és a két óra egyforma. Az órák számokkal jelenítik meg az időpontokat és egymással szinkronban járnak. Ránézünk az órára az A űrhajóban és látjuk, hogy t₁ időpontot mutat. Feltételezzük, hogy ránézésünk és az óra t₁ időpontbeli állása egyidejű. Ekkor küldünk egy jelet N.N. úrnak a B űrhajóba, aki amikor veszi a jelet ránéz az ő órájára, és megállapítja, hogy az ő órája a B űrhajóban t₂ időpontot mutat. (Mint korábban említettem, ezek a mérési értékek számok.) Amikor N.N. úr megkapja a jelet válaszol nekünk, és mi a válaszát a mi űrhajúnkban t₃ időpontban kapjuk meg. Amennyiben B űrhajó nincsen tőlünk nagyon távol, akkor t₁ és t₃ között olyan kicsi az eltérés, hogy az elhanyagolható, és ezért azt mondjuk, hogy t₁ = t₃. Ebben az esetben arra következtetünk, hogy t₁ egyidejű t₂-vel, amit tömören úgy fejezek ki, hogy a két időméréshez kapott számok azonosak, azaz t₁ = t₂. (Amennyiben az órák nem számokkal, hanem más jelekkel mutatnák az időt, akkor az azonosság reláció helyett csak ekvivalencia relációt írhatnánk.) Ebben a helyzetben bizonyos lehetek abban, hogy amikor én most látom, hogy az órám t₁-et mutat, akkor N.N. úr órája is t₁-et mutat, feltéve hogy az ő órája is számokat használ az idő jelzésére. Eddig a pontig egyezik meg a fizikus és filozófus érdeklődése. Eddig a pontig érvényes a köznapi gondolkozás az időről.

A modern fizika fölismerte, hogy megváltozik a helyzet ha B űrhajó tőlünk nagyon távol van, nagy sebességgel halad vagy egy nagy tömegű égitest közelében annak gravitációs terébe kerül. Ebben az esetben a B űrhajóban lévő óra lassabban jár mint az A űrhajóban lévő, és a két űrhajóban lévő óra által meghatározott idő-skála összekapcsolása sem egyszerű. Ekkor már nem triviális az egyidejűség értelmezése a két űrhajó viszonylatában, mivel jókora időbe telik, mire a jel eljut az egyik űrhajóból a másikba. Az ilyen problémák számszerű összefüggései érdeklik a fizikust az idővel (és a térrel) kapcsolatban. Ezeknek a számszerű összefüggéseknek a megfogalmazása olykor már csak kevesek által érthető matematikai nyelven történik, és magasabb szintű matematikai tudást feltételez.

A filozófus érdeklődése más. Őt a fogalmak jelentése és a létezés kérdései érdeklik. Mit jelent a ’múlt, jelen jövő’, melyik létezik ezek közül, megfordulhat-e az idő iránya, vissza mehetünk-e az időben? A filozófiai válasz keresése közben azonban érdemes alkalmazni a modern fizika azon felismerését, hogy az egyidejűség reláció, valamint, hogy a tudomány modelleket alkot, úgy ad magyarázatot. Ha van modellünk amelyik képes ábrázolni a ’múlt, jelen és jövő’ fogalmait, akkor rendelkezésünkre áll a fogalmi értelmezés alapja is, és a visszafelé múló idő fogalma is jobban érthető. Ha az egyidejűség reláció, akkor a ’múlt, jelen és jövő’ fogalmai mélyebb elemzésben relációs fogalmak, csak a köznapi gondolkozás kezeli ezeket tulajdonságként, egyargumentumú predikátumként. (Több filozófiai probléma is a helytelen fogalmi keret alkalmazásából fakad, amikor nem veszi észre a filozófus, hogy viszonnyal és nem tulajdonsággal van dolga.)

Az alapvető fizikában nincsen olyan fogalom, hogy ’jelen’ – mint tulajdonság (egyargumentumú predikátum). A csillagászat vagy a fizika tudományában csak időpontok, intervallumok, vonatkoztatási és koordináta rendszerek vannak, valamint az időpontok előbbi-későbbi vagy egyidejűségi relációja, valamint az idő mérése és annak mennyiségi viszonyai. Ezzel szemben a hétköznapi józan ész azt súgja nekünk, hogy csak a jelen létezik, a múlt már nem, a jövő pedig még nem. A newtoni ’F=m×a’ formula, amely alapösszefüggés a klasszikus mechanikában, tartalmazza az idő fogalmát. De ebben sincsen szó a jelenről, csak időbeli viszonyokról, relációkról, az m tömegű test adott rendszerben való gyorsulásáról, a rá ható F erő hatására. De akkor mi az a mindenkori jelen, amelyben benne élünk és folyamatosan változik, megállíthatatlanul belehull a múlt mélységes mély kútjába, és állandóan frissül a jövő egy szeletével?

Amikor a jelenről beszélünk, gyakran valaminek, egy folyamat szeletének tekintjük, de más felfogásban a ’jelen’ nem egy dolog – nem individuum név a logikai grammatikája – hanem egy tulajdonság vagy reláció, mégpedig az idő tengerén. De ha ez így van, akkor vajon lehet-e definiálni a ’jelen’-t valamilyen módon, pusztán a fizika által is használt fogalmakkal? (És itt nem spekulatív, álmélységekben tetszelgő szósalátákra gondolok, értelmetlen szóvirágokra vagy költői metaforákra, hanem logikailag precíz, formálisan korrekt és tartalmilag adekvát definícióra.)

Semmi akadálya annak, hogy a térben egyazon helyen maradj, ne mozdulj egy merev testhez képest, miközben múlik idő. Az viszont lehetetlen, hogy egy merev testhez kötött időben megállítsd az időt, egyazon helyen maradj és az idő ne múljon. Ki lehet ezt fejezni függvényekkel vagy formulákkal? A válasz attól függ, hogy a ’jelen’ tulajdonság-e vagy reláció.[ii]

Relációs definíció

Tulajdonságként nem lehet definiálni sem a ’jelen’-t, sem az idő múlását, csak a szavak jelentésével lehet ezeket kifejezni, csak a jelentéssel lehet a jelen illékonyságára és az idő kérlelhetetlen múlására utalni. Relációként viszont lehet definiálni, erről lesz most szó. Ez azért van így, mert a statikus szöveg világa – a kézírás vagy a nyomtatott szöveg – nem időbeli létező, hanem lényegileg időben változatlan valami, eltekintve a szöveg hordozójának valóságos fizikai sérüléseitől, kopásától. Nyomban megváltozik a helyzet, ha pl. egy táblázatkezelő jeleníti meg az összefüggéseket a kibertérben, vagy egy program kód futása egy automata működése közben. Mivel ezek lényegi mivoltukban időbeli adatrögzítő eszközök, ezek képesek fölmutatni a mindenkori jelent, azt az időpontot, amikor az információ eljut az olvasójához. A nyomtatott könyvek világa nem ilyen, és ez a forrása a fizika eternalizmusának.

Relációként fölfogva, eternalista álláspontról úgy lehet kifejezni a ’jelen’ fogalmát, hogy alkalmazzuk a fizika egyidejűségi relációját: x-időpont-jelen-y-időponthoz képest, pontosan akkor, ha x és y egyidejű. Legyen egy adott koordináta rendszer időtartományán értelmezett a „nem későbbi mint” reláció. Ekkor így definiálható a ’múlt, jelen és jövő’ relációs fogalomként, bevezetve a ’≤’ bináris relációt infix írásmódban fölírva:

x ≤ y := x nem későbbi mint y. (Természetesen egy adott rendszerben értendő.)

Ez egy antiszimmetrikus tranzitív reláció. Ezt fölhasználva természetes nyelvi kifejezéseket formális logikai eszközökkel definiálunk:

x múltbeli időpont y-hoz képest := x ≤ y & ~y ≤ x

x jelen idejű időpont y-al := x ≤ y & y ≤ x

x eljövendő időpont y-hoz képest := y ≤ x & ~x ≤ y

Ennek a relációnak egy részletét úgy ábrázolhatjuk, hogy az időpontoknak egész számokat feleltetünk meg:

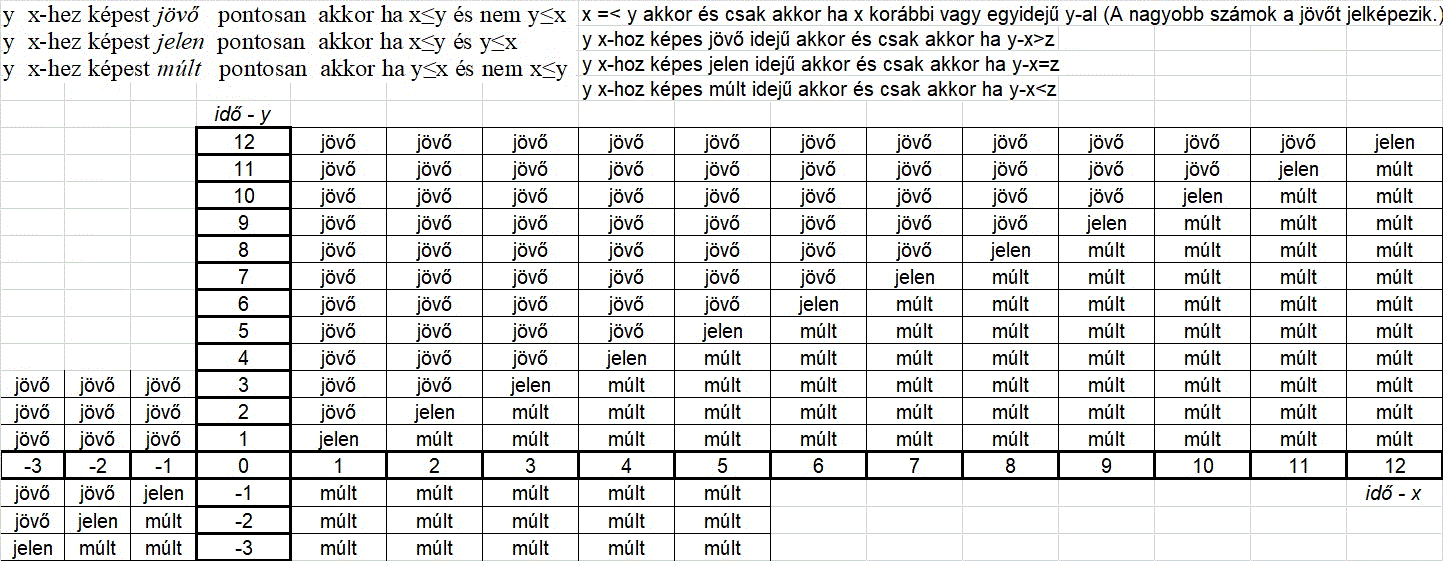
Ebben a megközelítésben egy időpont csak önmagához képest jelen, egy korábbi időponthoz képest jövő, egy későbbi időponthoz képest pedig már múlt. Még szemléletesebb a kép, ha mindezt grafikonnal mutatjuk be. Az alábbi ábrán a jövőbeli időpontok zuhannak alá a múltba. A távoli jövő mintegy pontként látszik, amint közeledik egyre szélesebb a horizont, majd amikor a múltba hullik, egyre távolodva ismét mindinkább a homályba vész:

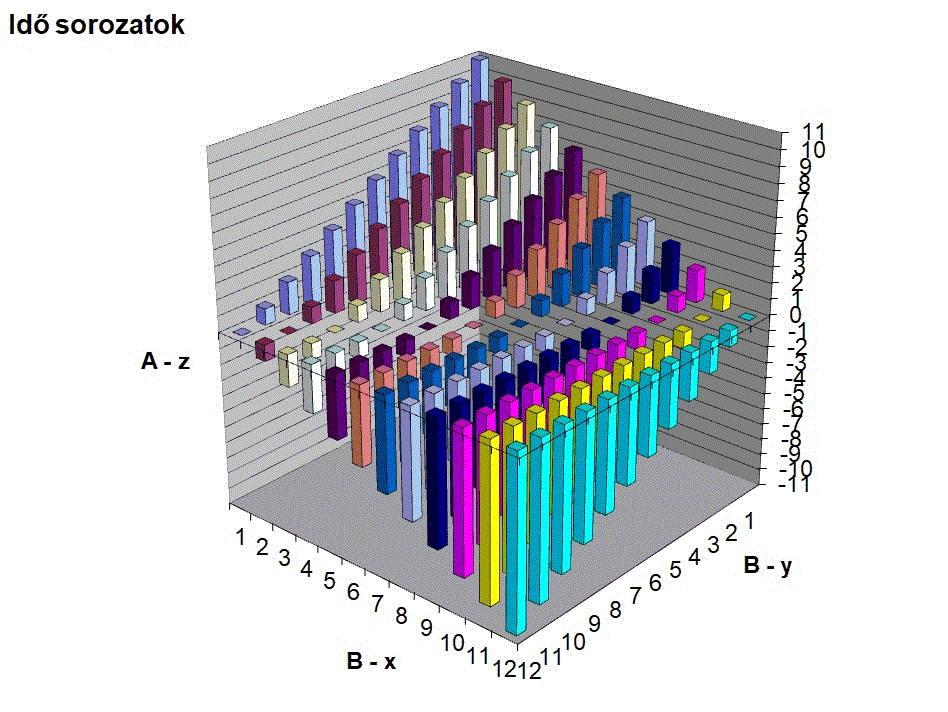
A relációs modell az idő következő tulajdonságait ábrázolja:

(1)  Az időpontok teljes parciális rendezést alkotnak a ≤ relációra nézve. (Lineáris rendezésnek is nevezik. £ antiszimmetrikus és tranzitív, és bármely két időpont között valamelyik irányban fennáll.)

(2)  Minden időpont múlt, jelen vagy jövő valamihez képest, de egyszerre csak az egyik. Ezek tehát ebben a felfogásban relációs fogalmak, és ezért nem zárják ki egymást, nincs közöttük ellentmondás.

(3)  Az idő irányát egyrészt megadhatjuk szemantikai interpretációval – pl. a nagyobb számok későbbi időpontok – másrészt utalhatunk rá a hátrafelé múló idő különös jelenségeivel.

(4)  A téridőben ábrázolható a visszafele múló idő is, de ekkor egy objektum több példányban is megjelenik. Ilyenkor az objektum helye nem függvénye az időnek, egyazon időpontban több helyen is lehet.

A relativitáselmélet szerint nincsen távolhatás, és a jelenidejűség ebben a keretelméletben ezért nem abszolút, hanem relatív, pontosabban relációs fogalom. Továbbá a relativitáselmélet szerint csak egy korábbi esemény hathat egy későbbire. (A kvantumfizikában ez másképp van – és ez egy megoldatlan problémája a fizikának. Az egyesek által fölvetett visszafelé forduló idővel most nem foglalkozom, korábban már megtettem.) A filozófia számára a létezés a kérdés, a lét a tét ebben az esetben is. Ha ugyanis csak egy korábbi esemény hathat egy későbbire, az másképp fogalmazva azt jelenti, hogy csak a múlt egy tartománya hathat a jövő egy tartományára. De ha ez így van, akkor mind a múlt, mind a jövő létezik, hiszen ha van valami a múltban ami hat, és van a jövőben, amire hat, akkor mind a múlt mind a jövő létezik. Ez viszont a józan ész prezentista felfogásának ellentmond. A fizikát ez nem zavarja, mert az a mindennapi gondolkodással szemben eternalista. Mondok egy példát, hogy érthetőbb legyen miről van szó.

S választottunk magunknak csillagot

Valamikor 1845 őszén (szeptember 26 és október 7 között), Borjádon Petőfi Sándor ül a négyökrös szekéren Erzsikével, akivel együtt választanak maguknak egy csillagot.[iii] Bizonyára nem gondoltak arra eközben, hogy a csillag, amit kiválasztottak, valójában ama csillag egy sokkal korábbi állapota, és a csillag abban az időpontban amikor ők az ökrös szekéren ülnek, talán már sokkal haloványabb fényű, talán már nem is létezik. Mindez persze itt a földön csak nagyon sokára lesz látható – és most ne feszegessük azt a kérdést, hogy mit jelent a csillag állapotának az ökrös szekér zötykölődésével való egyidejű állapota? Bárhogy is van, kettejükre egy múltbeli állapot gyakorolt hatást, közvetve ez hívta elő ama híres költeményt, és a költemény meg ránk az utókorra hat azzal, hogy örömet okoz. Így hat a távoli múlt a jövőre. De mindennek csak akkor van értelme, ha valamilyen értelemben nem a csak a jelen, hanem a múlt és a jövő is létezik.

Rövid kitérőt kell tegyünk, mert felmerül itt egy kézenfekvő ellenvélemény.[iv] A költő és szerelme talán nem a csillagot látta, hanem a csillag egy korábbi állapotából kiinduló fényt, amelyik most ért az ő látóterükbe. Ebből az következik, hogy nem csillag egy korábbi állapota hat rájuk, hanem a fény részecskéknek a látóterükbe érkező jelenbeli állapota hat kettejükre. Ha ez az ellenérv jó, akkor általánosan is érvényes. Sándort nem Erzsike szépsége ejti rabul, hanem azok a fény részecskék, melyek Erzsikéről kiindulnak. Legyünk következetesek, és menjünk tovább. A két emberre nem a fény részecskék hatnak, hanem a saját érzékleteik, melyek a részecskék hatására jönnek létre. Ezen a ponton viszont visszahőkölünk az ellenérv következményeitől: honnan tudjuk mindezt, ha nincsenek anyagi tárgyak, melyekből a fény részecskék kiindulnak? Ha az érzéklet hat ránk, az érzékletre a látvány, a látványra a fény részecskék korábbi téridőbeli állapotainak a hosszú sorozata, amelyik végül a csillag korábbi állapotához ér, akkor nem jó az ellenérv. Azért nem jó, mert a ’hat’ reláció nem intranzitív reláció, így a részecskék hatása nem cáfolja, nem zárja ki a csillag korábbi állapota hatását. Ha a fény hat Sándorra, a fény részecskékre pedig annak korábbi állapota, annak korábbi állapotára a még korábbi állapot, végül a csillag egykori állapota hat a belőle kiinduló fény részecskékre, akkor a tranzitivitás következtében, a csillag korábbi állapota hat Sándorra. Mindkettő igaz. A valóság ugyanis többféle nyelven is leírható. Leírható a tárgyak és leírható az érzékletek vagy jelenségek nyelvén is. A korábbi megfogalmazás ’látás’-ról és nem ’érzékelés’-ről beszélt. A költő és szerelme látja a csillagot és érzékeli a fényt, melynek részecskéi bennük érzékleteket hoznak létre. A ’látni’ eredmény ige, az ’érzékelni’ folyamat ige. A csillagokat látjuk, a fotonokat érzékeljük. Ha rosszul érzékelek, akkor rosszul látok, és esetleg káprázik a szemem. Látni vélem ama csillagot, amelyik nincs is ott, tehát valójában nem látom a csillagot, csak azt hittem, hogy látom a csillagot, mivel rosszul érzékeltem valamit. Ezért a költő helyesen mondja: „Választottunk magunknak csillagot.” és nem ezt: „Választottunk magunknak egy éppen a látóterünkbe érkező foton nyalábot.” Gondoljunk bele, a költő szemébe más fény részecskék érkeznek mint szerelme szemébe, és ha elfogadnánk a szenzualista filozófiát, akkor nem választhatnák ketten, egyazon csillagot!

Fönnmarad azonban a korábbi probléma lényege. Petőfi Sándor ül az ökrös szekéren édes kettesben az ő Erzsikéjével, és bizonyosan szívesen megállította volna az időt, megállította volna a jelent, ha ez lehetséges lett volna. Csakhogy nem volt lehetséges, az idő kérlelhetetlenül múlt, és a költő ideje is rohant előre ama végzetes csatamező felé. Ezt a tényt azonban semmilyen formulával vagy grafikonnal, ábrával nem tudjuk kifejezni, csak a szavak jelentésével, ami az olvasó hallgatólagos tudására apellál. A mi fenti két ábránk sem tudja kifejezni, hogy az idő megállíthatatlanul múlik, csak a viszonyokat tudjuk ábrázolni. Valójában az idő irányát sem mutatják az ábrák, miképpen azt a matematikai formulák sem tudják kifejezni. (A fizika formuláinak jelentése van, azokkal más a helyzet.) A tudomány az időt mintegy geometrizálja, térbeli viszonyként ábrázolja az előtte-utána viszonyt. Ez tehát a térré vált idő. Viszont a bolygó pályák ábrázolása önmagában még nem tér-idő szemlélet.

„Ha egy tömegpont mozgását olyan koordinátarendszerben ábrázoljuk, amelyben a koordináták között az idő is szerepel, akkor a pályát világvonalnak hívjuk. Az egyenes mentén történő mozgás s=ƒ(t) ábrázolása világvonal, a Kepler-ellipszisek azonban, amelyek az x,y síkban helyezkednek el, nem azok. Ez utóbbiak akkor lesznek világvonalak, ha a síkra merőlegesen az időtengelyt is felvesszük. Ekkor az ellipszisek csavarvonalakká húzódnak szét.”[v] Ennek szellemében járunk el. Egy diszkrét tér-idő pontokból álló piciny véges világban modelláljuk egy pont egydimenziós haladását az időben. Mivel nem a számszerű összefüggésekre koncentrálunk, hanem a logikai-fogalmi összefüggésekre, ezért megengedhető a diszkrét tér-idő feltételezése.

Az idő fogalma a kibertérben, táblázatkezelő formában

Ebben a véges, egydimenziós világban 19 hely van, és világ ideje 15 pillanatból (ütemből, diszkrét időegységből) áll. Az alábbi pillanatfelvételen az ötödik időpillanatban az 5-ős számú helyen vagyunk. A következő pillanatban tovább megyünk, majd egy kicsit megpihenünk. [vi]

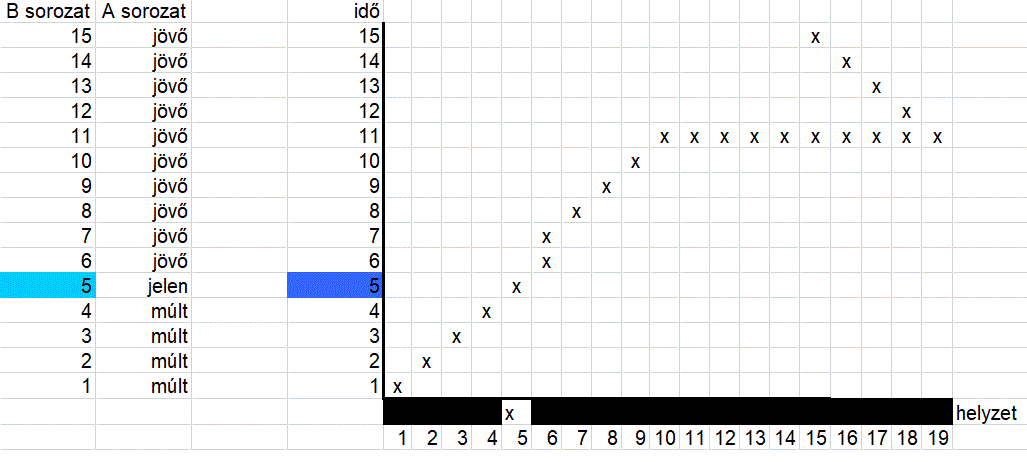
Utána tovább haladunk a 10-es helyig, ahol viszont őrült száguldásba kezdünk, és végtelen sebességgel elrepülünk a világ végére, ami a 19-es hely. Ott azonban visszafordulunk egészen a 15-ös helyig, ahol bevárjuk az idők végezetét. Most amikor ezt a szöveget olvassuk, minderről csak pillanatfelvételt látunk, nem is láthatunk mást a statikus szöveg világában. Megváltozik a helyzet, ha mindezt a kibertérben nézzük. Töltse le az olvasó az alábbi táblázatot, és nyissa ki.

http://ferenc.andrasek.hu/modellek/time-series-hu3.xlsx vagy

http://ferenc.andrasek.hu/modellek/time-series-hu3.xls

A számítógép F9 gombjának lenyomására múlik az idő, és változik a mindenkori jelen. A modell mutatja, hogy épp hol vagyunk, melyek a korábbi időpontok, és melyek a jövőbeliek. A modell ismeretében mindentudók vagyunk, tudjuk előre a jövőt, és teljesen ismerjük a múltat. Az x jelek máshova írásával szabadon megváltoztathatjuk az objektum pályáját, történetét. A táblázat összes lehetséges kitöltése meghatározza az objektum összes lehetséges történetét. Külön rögzíthetjük, hogy a végtelen sebességet leszámítva, az objektum helye függvénye az időnek. Ebben az esetben az objektum egyszerre csak egy helyen létezhet, nem sokszorozódhat meg, nem létezhet egyszerre több példányban. Ebből az következik, hogy nem haladhat visszafelé az időben. Ilyen módon pusztán formális matematikai kikötéssel megkülönböztethetjük az időben visszafelé haladást az idő természetes irányától. (Erre utaltam korábban.) Az összes lehetséges ilyen út-idő függvényre korlátozva az objektum lehetséges történeteit, a függvények halmazának lesz egy eleme, amelyik pontosan leírja az objektum történetét, a múltját és a jövőjét egyaránt. Ez a függvény, amelyik tehát a jövőt is leírja, matematikai okokból szükségszerűen létezik. Azonban van itt egy gyakori és súlyos félreértés a filozófusok között: az un. „logikai determinizmus”-ban való hit. Valójában nincs ilyen determinizmus. Ontológiai szakadék tátong a logikai-matematikai törvények világa és a fizikai események világa között. Az objektum történetét nem az határozza meg, hogy a jövőjét leíró függvény szükségszerűen létezik, hanem az az oksági kapcsolat, ami a modell világában lévő függvény – a x-ek egy grafikonja – és a modell valóságos időbeli működése között van. Az oksági kapcsolat, a modell mint automata determinisztikus működése nélkül, a függvény nem befolyásolná az eseményeket, nem befolyásolná a jövőt. Csak azért határozza meg a x-ek által leírt grafikon a modell eseményinek történetét, mert ez egy ilyen modell, így működik. Lehetne másmilyen is, olyan is, amelyik valószínűségi alapon működik és nem determinisztikusan. Ekkor már nem látnánk előre a jövőt a modell világán belül.

Nyitott kérdés, hogy a modell eternalista személetű-e. A kibertérben az objektum mindig ott van ahol a jelenben van, ez a prezentizmust támasztja alá. Ugyanakkor teljesen meghatározott az objektum története, amit a grafikon ábrázol. Utóbbi inkább az eternalizmust igazolja.

A táblázatkezelő modell az idő következő tulajdonságait jeleníti meg a kibertérben:

(5)  Az időpontok teljes parciális rendezést alkotnak a ≤ relációra nézve.

(6)  Minden időpont múlt, jelen vagy jövő a mindenkori jelenhez képest, de egyszerre csak az egyik. Ilyen módon ebben a modellben ezek tulajdonságok és nem relációk.

(7)  Múlik az idő minden egyes gombnyomás inputra, tehát az időnek iránya van a modellben.

(8)  Megjelenik a mindenkori múlt, jelen és jövő, miközben minden egyes gombnyomásra múlik az idő a modellen belül. Utóbbi kiváltható lenne egy digitális órával is, de az nem tenne hozzá semmit a magyarázat szemléletességéhez.

(9)  A modell képes ábrázolni a visszafelé múló időt is, az objektum megsokszorozódásával. (Ennek tárgyalásával majd egy másik írásban foglalkozom.)

Összefoglalás     

Az idő filozófiai magyarázatai közül az a jobb, amelyik az idő több tulajdonságát képes ábrázolni. A kibertér nyújtotta lehetőségek felülmúlják a statikus szöveg lehetőségeit, mert időbeli változásokat is képesek megjeleníteni. A kibertérben az idő több tulajdonsága modellálható, mint a szöveg vagy a formulák világában. Következésképpen egy adekvát táblázatkelő modell nagyobb magyarázó erővel rendelkezik, mint a puszta szó.[vii] 

[i] Kereszty István és Lányi Viktor fordítása. Figyeld meg, hogy a fizikának ez a két fogalma idézőjelek nélkül szerepel a szöveg e részében, helyesen mutatva, hogy most használjuk, és nem említjük ama két alapfogalmat. Nem a fogalmak összefüggéséről van szó, hanem arról amit jelentenek, ami a nyelven kívüli világ összefüggése. Ezt követi az egyszeres idézőjelek használata a továbbiakban. Az egyszeres idézőjel egyfajta metanyelvi operátor, a használat és említés különbségét fejezzük ki vele. Alkalmazása kockázatos, nagy körültekintést igényel, mert könnyen ellentmondásokat generál.

[ii] Egy adott időskála pontjai közötti rendezés logikai tulajdonságait könnyedén ki tudjuk fejezni pl. az időpontoknak a számokhoz való rendelésével, de hogy melyik szám a korábbi és melyik a későbbi, a pusztán megállapodás kérdése.

[iii] http://magyar-irodalom.elte.hu/sulinet/igyjo/setup/portrek/petofi/negyokr.htm

[iv] Erre Julius Ecktsein kolléga hívta föl a figyelmemet.

[v] Hraskó Péter, A relativitáselmélet alapjai (2009) Typotex, Budapest, p. 70. jegyzet

[vi] Feltételezem, hogy az olvasó ismeri az idővel kapcsolatos alapvető álláspontokat, így pl. az A sorozat vagy a B sorozat fogalmát is. A locus classicus szöveg John M. E. McTaggart: Miért nem valóságos az idő in. Farkas Katalin – Huoránszki Ferenc, Modern metafizikai tanulmányok (2004) Eötvös Kiadó, Bp. c. tanulmánya, megtalálható a neten: http://www.szv.hu/cikkek/miert-nem-valosagos-az-ido

Nekem egy korábbi írásom sok olyan aspektusával foglalkozik a problémának, amire itt nem tértem ki:http://ferenc.andrasek.hu/pdf-papers/time/a-jelenlet-talanya4.pdf

Javaslom elolvasni Ujvári Márta: Idő, igeidő és McTaggart érvének »indexikus hibája« (2001) Magyar Filozófiai Szemle 45. évf. 1-2, p.55-81 c. dolgozatát. Megtalálható a neten: http://epa.oszk.hu/00100/00186/00008/5ujvari.html Ennek végén irodalomjegyzék is található a további tájékozódáshoz. Természetesen angolul óriási irodalma van a témának, még külön egyesülete is: Philosophy of Time Society.

[vii] A poszt szövege innen tölthető le:http://ferenc.andrasek.hu/pdf-papers/time/terre-valt-ido.pdf

Herbert von Karajan: Wagner - Parsifal, 'Overture'