Ha már az előző poszt kapcsán szóba került másképp is elmagyarázom az események valamint az ontológiai kategóriák fogalmát. Persze csak az alapgondolatot. Nem olyan bonyolult ez.

Ontológiai kategóriákat minden épeszű ember használ, bele van drótozva a nyelvbe, a józan ész gondolkozásmódjába. Gyerekkorunkban sokan játszottunk Bar Kochba játékot. Az egyik játékos gondolt valamire, a másiknak pedig ki kellett találni kérdések és válaszok logikus rendszerével, hogy mire gondolt, miközben csak igennel és nemmel szabad válaszolni. (Esetleg valamilyen harmadik lehetőség is megengedett.) Az a rendszer, a szavaknak-fogalmaknak az a hálója, amivel próbáljuk kihalászni a létezők tengeréből, hogy mire gondolt a játszótársunk, az nem más, mint az ontológiai kategóriák egy természetes rendszere. Ez a rendszer a fogalmak nagyon átfogó csoportjával indul. Ilyenekkel: élőlény vagy élettelen dolog, fogalom vagy tárgy, létező személy vagy kitalált személy, anyagi tárgy vagy esemény. Sokféle kérdezési stratégia elképzelhető, nincsen egyetlen egyedül üdvözítő kérdezési séma. Az a lényeg, hogy fokozatosan szűkítsük a kört. A filozófusok nagyon sok ilyen rendszert kidolgoztak, az ő rendszereik gyakran sajátos fogalmakat, vagy a köznapi szavak sajátos értelmezését használják. A Bar Kochba játék esetén lényeges, hogy a szavakat-fogalmakat egyformán értse a kérdező és a válaszoló. Ha más ért a kérdező és a válaszoló egy szón, kifejezésen, akkor annak használatát kerülni kell. Ha pl. a játékosok nem járatosak a filozófiában, akkor szamárság azt kérdezni, hogy valami partikuláré-e vagy univerzálé netán trópus? Hiszen ezeknek nincsen jelentése a köznapi nyelvben. De más szavaknak, amelyeket a filozófia is használ, van jelentése. Ilyen pl. az esemény vagy anyagi tárgy. Itt arra kell ügyelni, hogy köznapi értelemben a lassú folyamatokat általában nem tekintik eseménynek, sem az állapot-időpont párokat, amelyeket pl. a fizikában némelyek eseménynek neveznek. Ha monista vagy akkor szintén kerülni kell a saját előfeltevéseidet. Nem visz előbbre, ha azt kérdezed: Isten teremtménye? Anyagi létező? Nem írhatod elő, hogy játszótársadnak veled megegyező világnézete, vallási hite legyen.

Ez a játék nem puszta szórakozás, gondolkozni tanít, filozófiai gondolkozásra tanít, és használják a különféle tudásalapú informatikai rendszerek is. Itt kapcsolódik az ontológia, a filozófia a gyakorlati tudományokhoz. De ez más tészta, most nem foglalkozom vele részletesebben.

A játékosok többnyire bölcsen körül szokták határolni a kérdések lehetséges tárgyának a körét. Ellenkező esetben jóval nehezebb a játék, bár nem lehetetlen. Lássunk egy példát. Valaki a nevezetes Bastille börtönre gondol, egy másvalaki pedig ama épület ostromára. Az első egy épület, egy fizikai tárgy, a második viszont egy fontos történeti esemény. Honnan látszik, hogy ezek alapvetően különböző dolgok? Onnan, hogy a kérdések elágazási pontjai a fogalmi háló tövéhez közel helyezkednek el. Ez az amit a filozófiában úgy neveznek, hogy a Bastille ostroma más ontológiai kategóriába tartozik mint a Bastille.

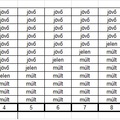
A középiskolai matematikát nem meghaladó fogalmakra építve a korábbi kertkapus példa alapján pontosabban is elmagyarázom az esemény és tárgy különbségét. Az én kertkapumat egy ügyes lakatos készítette vas szerelvényekből sok évvel ezelőtt. Időközben a kaput átfestettük, kicseréltük a benne lévő zárat, és az azt rögzítő csavart. Mindeközben kétségünk sem maradt, hogy az én kertkapum bár, itt ott megváltozott, azért ugyanaz a kertkapu maradt, a változások nem érintették az önazonosságát. Az egyszerűség kedvéért tételezzük fel, hogy a kertkapunak csak egyetlen tulajdonságát, egyetlen jellemzőjét vizsgáljuk, nevezetesen azt, hogy milyen α szöget zár be a kerítés síkjával. Ha nulla fokot, akkor a kapu zárva van, ha közel száznyolcvan fokot, akkor teljesen ki van nyitva, ha csak tíz fokot, akkor valaki elfelejtette becsukni és résnyire nyitva van. Namármost ez a szög minden időpontban fölvesz egy és csak egy értéket, azért a kapu helyzetét leírhatjuk egy függvénnyel az időben. A függvény értelmezési tartománya az időpontok rendezett halmaza, értékkészlete pedig a szögek nullától száznyolcvan fokig terjedő halmaza. A szimbolikus logika szabatos nyelvét fölhasználva pontosan megfogalmazhatjuk, hogy mi a különbség az esemény és tárgy között. Jelölje az én kertkapumat ’a’ individuumnév, az időpontok rendezett halmazán legyen értelmezve egy ’t’ változó, melynek egyes értékei legyenek t₁, t₂ stb. A szomszédom kertkapuját jelölje ’b’ individuumnév. Ekkor a kertkapuk történetér leírja egy ’f’ függvény, ahol az én kertkapum állapota valamely tetszőleges t időpontban f(a,t). A szomszédomé ugyanekkor értelemszerűen f(b,t). Az hogy a kapum csukva volt ma hajnalban ekkor így fest: 0=f(a,ma_hajnal) A kertkapumat kinyitottam tegnap reggel, melyet egy f₁ függvény írt le, és kinyitottam ma is, amit egy másik f₂ függvény. Ha egyforma módon nyitottam ki tegnap és ma is, akkor a két függvény grafikonja fedésbe hozható, ha nem hozható fedésbe, akkor az egyik esetben lassan nyitottam ki, míg a másik esetben gyorsan. De bárhogy is történt, f1≠f2 azaz a két esemény különbözik egymástól. És nyilvánvaló az is, hogy f1≠a és f2≠a azaz mindkét esemény különbözik a kertkaputól, a tárgytól. A kettőt összekeverni kategória hiba. Az időt durva felbontásban tekintve ezt a függvényt táblázattal is bemutatom az én ’a’ jelű kapum esetén. Nem írom oda a szögek mellé, hogy ez a ’a’ jelű kapuhoz tartozik, mivel ez nyilvánvaló:

Figyeld meg, hogy a tegnap reggeli állapot-időpont pár akkor is különbözne a maitól, ha mindkettő azonos szöget tartalmazna. Azért különböznek, mert az időpontok különböznek. Figyeld meg azt is, hogy a táblázat véletlenül megegyezhet a szomszéd kapuja eseményeivel, akkor is az egy másik esemény.

Mi következik mindebből? Vajon a fentiekkel bebizonyítottam, hogy léteznek események? Sajnos nem. Éppúgy tagadhatod az események létét, mint azt is, hogy olyan összetett fizikai tárgyak léteznek, mint a kertkapu. Nem mondom, hogy engem meggyőzöl, de ez a lehetőség nyitva áll. Mi az amit akkor bizonyítanak a fenitek? Azt bizonyítják, hogy ha léteznek események, és ha léteznek fizikai tárgyak, akkor ezek különböző ontológiai kategóriákba tartoznak, amit az mutat, hogy az őket leíró formális nyelv más nyelvtani kategóriát használ a leírásukra, az első esetben függvényeket, a második esetben individuumneveket. Hogy egy korábbi posztomra utaljak, a kertkapu mint fizikai tárgy, annak nyitása mint esemény, bizonyosan létezik a létezés belső értelmében, azaz a keretelméleten belül, de neked nem kötelező ezt a nyelvet elfogadni. Vajon gondolataink logikai struktúrája összefügg a valóság metafizikai struktúrájával?