Az előző posztban a tudás klasszikus definícióján azt értettük, hogy a tudás igaz, igazolt hit. (Justified True Belief= JTB elmélet). A problémának ez a megközelítése a hit felöl közelít a tudáshoz. Azt keresi, hogy mi szükséges a hiten felül ahhoz, hogy tudjunk. A filozófiai írók egy meghatározást, szükséges és elegendő feltételeket kerestek, amelyek ha teljesülnek, akkor bizonyosan tudunk, nem csak hiszünk. Egy definíció kétirányú következtetést jelent, ezért a tudás klasszikus definíciója szerint két érvényes következtetési sémánk van:
- Ha s tudja p-t akkor: s hiszi p-t, p igaz és p igazolt.
- Ha p-igaz, p-igazolt és s-hiszi p-t akkor: s tudja p-t.
Senki nem vitatja (i)-et, Gettier a második tételt, (ii)-t cáfolta meg. (i) szerint ha tudom, hogy p, akkor hiszem, hogy p, p igaz és azon felül igazolt is. Tehát ha tudom, hogy p, akkor lehetetlen, hogy p hamis legyen, hamisságot nem lehet tudni. Hinni viszont lehet az igazságban és a hamisságban is, miközben egy hamisság nem lehet igazolt. Utóbbi állítást érdemes jól megérteni. Ha q-ból logikailag következik p, és q igaz, akkor p igazolt: ezt értjük igazoltságon. (Nem zárjuk ki a logikaitól eltérő, pl. érzékelésen, tapasztaláson alapuló igazolás lehetőségét. Ilyen eset:honnan tudod, hogy jönnek? Jó a szemem, kinéztem az ablakon, és láttam őket a távolban közeledni.) Ha viszont q hamis, és p következik q-ból, akkor nem beszélhetünk p igazolásáról q alapján. Természetesen más tény igazolhatja p-t. Előző írásomban ezzel már foglalkoztam.
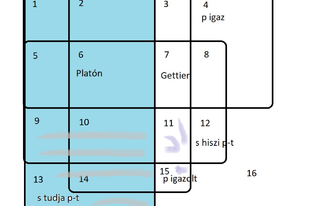
A korábbi posztban ismertetett, a klasszikus tudás definíciót cáfoló érv négy fogalom egymáshoz való viszonyát tárgyalta: a hitét, az igazságét, az igazoltságét és a (propozicionális) tudásét. Ezek közül a ’hit’ és a ’tudás’ relációs fogalmak: s – hiszi p –t; s – tudja p-t; az ’igazság’ és az ’igazoltság’ viszont tulajdonságnak tekinthető. (Tekinthető nyelvhez, keretelmélethez között relációnak is, de ezen most felülemelkedünk.) A két relációs fogalmat is tekinthetjük úgy, mint ami az első argumentumukat rögzítve terjedelmeket határoz meg, a hitek és a tudások halmazát. Ilyen módon a hitek, tudások, igazságok és igazoltságok négy halmazát kapjuk, melyek egymással tizenhat féle viszonyban (relációban) lehetnek. Érdemes ezt Venn–diagrammal ábrázolni, és az összefüggéseket megvizsgálni. Megszámoztam a négy halmaz tizenhat féle kapcsolatát, metszetét, melyeket szekcióknak is nevezek. Az egyes halmazokat lekerekített sarkú téglalapok ábrázolják, a tudás halmazát kiszíneztem. A halmazok elemei propozíciók (kijelentések), melyek vagy igazak vagy hamisak. Gondoljuk át, hogy melyik tartomány mit jelent, és melyik tartomány szükségszerűen üres. Külön kérdés, hogy a „szükségszerűség” milyen fogalmát használjuk ilyenkor?
- Az igazságok az 1,2,3,4,5,6,7,8 szekciókban vannak,
- hiteink az 5,6,7,8,9,10,11,12 részekben,
- az igazolt kijelentések alkotják a 2,3,6,7,10,11,14,15 tartományokat,
- és végül tudásunk az 1,2,5,6,9,10,13,14 metszetekben található.
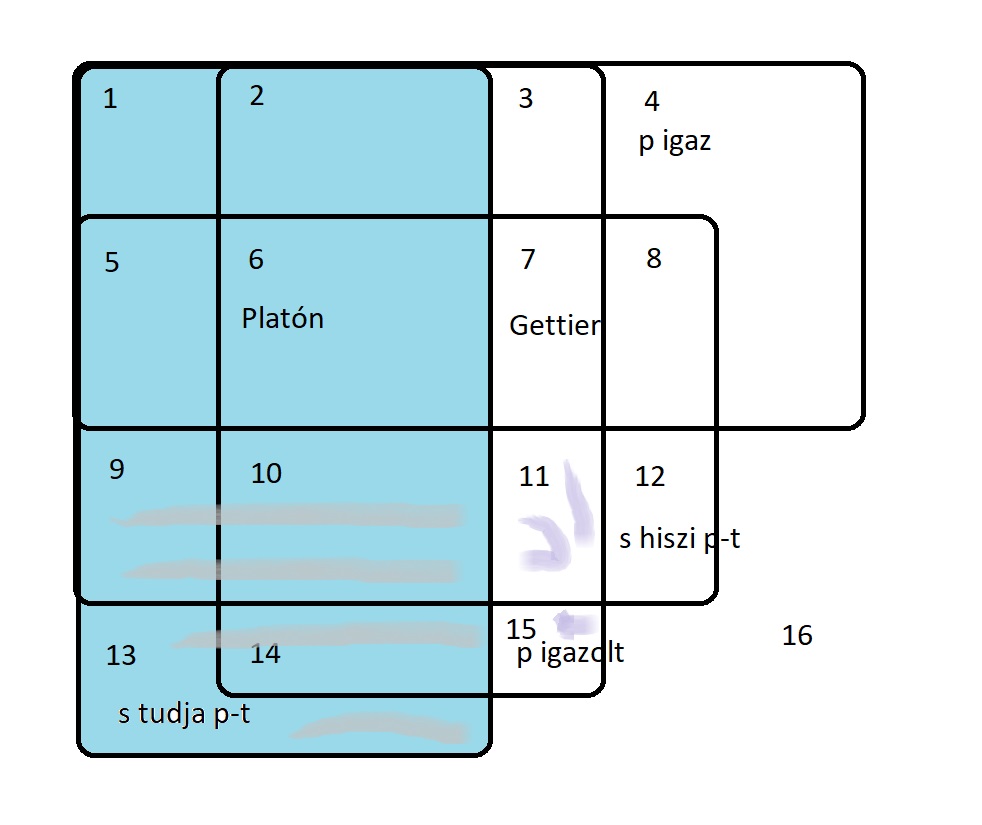
A 9, 10, 13 és 14 szekciók üresek, mert hamisságot nem lehet tudni, ezt jelzi a sraffozás. Más színnel sraffoztam a 11, 15 szekciót, mert hamisság sem lehet bizonyított. A 12-es szekcióban vannak azok a hamis kijelentések, amelyekben valaki hisz, a 8-as szekcióban pedig az igaz hitek szerepelnek. Számos igazság és hamisság ismeretlen előttünk, ezekben senki sem hisz, a 4 és 16 szekció ezt ábrázolja. Az 1-es szekció a senki által nem hitt, bizonyítatlan, de tudott igazságok – feltehetően üres – halmaza. A 2-es szekció szintén üres, mert ide tartoznának a tudott, de nem hitt kijelentések. Bár van olyan filozófus aki szerint ez tartomány lehetséges (Colin Radford). Előfordulhat, hogy miközben meglátunk valami számunkra felfoghatatlan jelenséget, pl. bűvészmutatványt, így szólunk: ez hihetetlen, látom, de nem hiszem el. A 3-szekcióban a senki által nem hitt, nem tudott, de bizonyított igazságok tartoznak. Van ilyen? Az 5-ik szekció a tudott, hitt, de nem igazolt igazságokat tartalmazza – ilyenek azok az esetek, amikor biztosan tudunk valamit, de már nem emlékszünk a tudásunkat alátámasztó igazolásra, bizonyítékra. Van olyan filozófus is (Pl. Alvin Goldman), aki szerint ez lehetséges.
És ezzel elérkeztünk a vita neuralgikus pontjához. A 6-os szekcióban vannak az igaz, igazolt hitek, melyeket tudunk, a 7-es szekcióban pedig az olyan igaz, igazolt hitek, melyeket nem tudunk. Gettier és követői szerint a 7-es szekció nem üres. A Venn-diagram mutatja, hogy az (i) következtetési séma episztemikusan érvényes, míg a másik (ii) séma nem érvényes, amennyiben Gettier ellenérve jó, azaz a 7-es szekció nem üres.
A poszt szövege innen letölthető. A befejező rész következik.