Anno 2012-ben írtam ezt az írásomat, kisebb javításokkal jelenik most meg.
************************************************************
Létezik-e az idő?
Érdekes, hogy a kérdés mindig a fizikai időre vonatkozik, és nem a szubjektív időre, melyet a pszichológia tanulmányoz, és melynek homályos fogalma jóval tágabb teret enged a spekulációnak. Talán azért van ez így, mert a fizikai idő létezésében való kétely radikálisabb és ezért feltűnőbb álláspont, ami némelyeknek vonzó, mivel éppannyira ellentmond a józan észnek, mintha valaki a távolság vagy a tömeg létezésében kételkedne. Bárhogy is van, sok tekintélyes filozófus tette föl ezt a kérdést, és ezért nem hiábavalóság a róla való elmélkedés.
Mindennek ami létezik vannak tulajdonságai, így kezdjük vizsgálódásunkat ebből az irányból.
Mik az idő tulajdonságai?
Sean Carroll hármat sorol föl:
- Az idő azonosítási pontokat nyújt, koordináta mely segít az események azonosításában, mintegy fölcímkézi univerzumunk történetét.
- Az idő az események közötti tartamot méri, az a fizikai jellemző, amit a pontos órák mérnek.
- Az idő egy közeg, melyen át mi élőlények magunk is haladunk.[i]
Tudjuk, hogy az idő múlik, és ezt hajlamosak vagyunk térbeli analógiákkal fölfogni. Ábrázoljuk egy számegyenessel az időt olyan módon, hogy a ’kisebb vagy egyenlő’ relációnak a ’korábbi vagy egyidejű’ reláció felel meg. Ekkor a nagyobb számok a jövőt, a kisebbek a múltat ábrázolják. Figyeljünk föl arra, hogy maga az ábrázolás időtlen. Sok filozófus számára jelentett és jelent ma is gondot annak megértése, hogy miképpen a mozgás írott szöveg részeként való leírása maga nem mozog, akképpen az idő írott szövegként való leírása sem visel időbeli jelleget. Írott, nyomtatott szöveg részeként a logikai-matematikai leírás időtlen, mivel a jelek nem mozognak a papíron. (Mindez alapvetően megváltozik a kibertérben, amire később visszatérek.)
Középiskolai fizikai tanulmányainkból tudjuk, hogy az idő kifejezhető a sebesség és út fogalmával. Válaszolhatjuk télen a gépkocsi fűtésére panaszkodónak, hogy öt km múlva fölmelegszik a motor, és beindul a fűtés. A relativitáselméletből pedig megtanultuk, hogy az egyidejűség, valamint a múlt és jövő viszonya csak térben közeli események esetén egyértelmű, távoli események esetén függ a vonatkoztatási rendszertől. Meddig mehetünk tovább az idő meghatározásában?
Az, hogy a számegyenest egyenes vonallal ábrázoljuk, puszta szokás, pszichológiai célszerűség, nem következik a számok fogalmából. Az, hogy a kétszeres fizikai mennyiségnek kétszer akkora szám felel meg, puszta szokás, lehetne másképp is, némely esetben pl. logaritmikus skálát használunk. A geometriai fogalmak, a tér fogalmai algebrai leírása interpretáció kérdése, semmiféle fizikai jellemző, sem a tér, idő, vagy tömeg és erő nem definiálható, nem vezethető vissza, nem redukálható tisztán logikai-halmazelméleti fogalmakra. A számokat mi hozzuk kapcsolatba a valósággal. A matematika és logika alkalmas nyelvet nyújt a fizika számára, de a matematikai-logikai nyelv interpretációja nem nélkülözheti a mérhető, fizikai fogalmakra való hivatkozást. Az idő fogalma esetén sem könnyebb a helyzetünk. A statikus nyomtatott nyelv világában csak leírható az idő némely tulajdonsága, és csak más fizikai fogalmak alkalmazásával definiálható. Ezzel szemben a kibertérben maga az idő múlása, külső események időbeli hatása – mint egy program inputja – is megjelenik a maga valóságában.
Abban a kérdésben nem dönt az idő matematikai ábrázolása, hogy a múlt folyik a jövő felé, vagy fordítva, a jövő zuhan folyamatosan a múlt mélységes mély kútjába. A kérdés eldönthetetlen, de nem is fontos. (Egy másik írásomban megmutatom, a múlt és jövő különbsége abban is megmutatkozik, hogy a szükségszerűség egy plauzibilis értelmezésében a múltra vonatkozó igaz tapasztalati kijelentések nem csak kontingens igazságok, hanem szükségszerűen igazak, ezzel szemben a jövő a lehetőségek világa.) Ami mostani vizsgálódásunk szempontjából lényeges, az az a meggyőződés, hogy a múlt megváltoztathatatlan.[ii]
Lét és idő
Tegyük fel, értjük mit jelent a kérdésben szereplő ’idő’ szó annak ellenére, hogy a létezését kérdésesnek tartjuk. Ezzel azonban még nem tisztáztuk a kérdést magát, hiszen korántsem nyilvánvaló, hogy mit jelent a létezés kérdése az idővel kapcsolatban.
Értjük mit jelent amikor Ada Kaleh sziget valamikori létezésére kérdeznek rá, és azt is tudjuk, hogy teljesen mást jelent, egy másodfokú egyenlet pozitív megoldásának létezése, és egy harmadik értelemben beszélünk létezésről amikor azt vizsgáljuk, hogy egy vallási nézetrendszeren belül elfogadott-e az angyalok léte.[iii] Azért beszélünk mindhárom esetben létezésről, mert az ezzel kapcsolatos állításoknak hasonló a logikai formája. A hasonlóság azonban csak addig tart, amíg meg nem fogalmazzuk, hogy milyen feltételek esetén igaz vagy hamis a három létezéssel kapcsolatos kérdés. A létezés tehát a logikai formán túl mást-mást jelent attól függően, hogy minek a létezése felől érdeklődünk. Értelmes-e egyáltalán az idő létezésére rákérdezni?[iv]
A filozófusoknak nincs egységes álláspontja arra nézve, hogy amennyiben egy nem létező dologról teszünk állítást, akkor az értelmetlen vagy hamis. Abban azonban egyetértenek, hogy egy nem létező dologról szóló mondat bizonyosan nem igaz. Ezért ha nem létezik idő, akkor az időt tartalmazó állítások vagy hamisak vagy értelmetlenek. Mondok egy példát, hogy jobban érthető legyen.
Egy nyomozó azt vizsgálja, hogy két térben közeli lövés egyidejű volt-e avagy eltelt közöttük valamennyi idő. (Ha nagyon távoli lett volna a két lövés, akkor a hang véges terjedési sebességéből kifolyólag a kérdés nem volna egyértelmű.) A nyomozó ezzel kapcsolatos feltevései értelmetlenné vagy hamissá válnak, ha valaki úgy gondolja, hogy az idő nem létezik. Nem csak a nyomozó feltevéseinek értelmessége válik kérdésessé. Semmivel sem abszurdabb azt állítani, hogy az idő nem létezik, mint ha valaki azt állítja, hogy távolságok vagy tömegek nem léteznek. Az idő épp úgy mérhető, miképpen a távolság vagy a tömeg, mindegyik alapvető fizikai jellemző. Ha valaki azt állítja, hogy az idő vagy a távolság nem létezik, akkor abból az következik, hogy a mérésükre készített szerkezetek nem mérnek semmit. Az is következik belőle, hogy olyan jelenségek sem létezhetnek, melyek léte időbeli, az időhöz kötött, mint amilyenek a hangok vagy fényvillanások. És ezen a ponton megválaszolhatjuk a kérdést, hogy milyen lenne egy idő nélküli világ: mozdulatlan, holt, sötét és hangtalan. Ebből azonban az is következik, hogy az idő létezését firtató kérdés értelmes, hiszen el tudjuk magyarázni minek esete állna fenn az egyik, és minek esete állna fenn a másik esetben. Csak meg kell vizsgálnunk, hogy hallunk-e hangokat, pendüléseket, csörrenéseket vagy koccintásokat, fényben vagyunk-e avagy teljes sötétségben, és máris tudjuk a választ: az idő létezik. Kevés dologban lehetünk olyan bizonyosak mint éppen ebben.
Miért van akkor, hogy oly sok kétségtelenül jelentős filozófus ennek az ellenkezőjét gondolta? Azért mert úgy vélték, hogy az idő létezését alátámasztó tapasztalataink csalókák, megtévesztenek bennünket. (Hasonlóképpen érvelt pl. az eleai Zenon is a mozgás lehetetlensége mellett.) Ingoványos filozófiai álláspont a tapasztalatok általában vett megbízhatatlanságára hivatkozó szkeptikus ismeretfilozófia, de most feltételesen fogadjuk el mégis.[v] Ám ha a tapasztalatok nem megbízhatóak az idő létezésével kapcsolatban, akkor nem létezésének igazolásával kapcsolatban is megbízhatatlanok. Amiből az következik, hogy tapasztalati érvek sem az idő létezése mellet, sem ellene nem meggyőzőek. Tehát ha valaki mégis cáfolni akarja az idő létezését, azt logikai érvekkel kell alátámasztania. Hogyan nézne ki egy ilyen bizonyítás?
Ezen a nyomon kell haladjunk. Találnunk kell egy biztos állítást, melynek igazságához nem férhet kétely, majd be kell bizonyítsuk, hogy az idő létezésének feltételezése ellentmond ennek a biztos állításnak. Mindebből indirekt bizonyítással – reductió ad absurdum érveléssel – az következik, hogy föltevésünk legalább egyik tagját el kell vessük, és az nem lehet más, mint az idő létezésébe vetett hit, mivel a másik állítás bizonyos. De mi lehet egy ilyen bizonyosság? Kéznél van a válasz, egy ilyen bizonyosság az, hogy semminek a fogalma nem lehet ellentmondásos, ha az idő fogalma mégis az, akkor az idő nem létezik.
Sajnos eme hitünket sem kerüli el a filozófiai kétely. Jómagam hajlanék arra a vélekedésre, hogy ha az idő vagy a mozgás jelensége nem írható le ellentmondásmentesen, akkor vagy a logikánk hibás, vagy elérkeztünk alkalmazásának korlátaihoz.
(Könnyedén kreálhatunk a létezést cáfoló szofizmákat relációs tulajdonságok abszolút tulajdonságként való kezelésével. Bebizonyíthatjuk, hogy a piszkavas nem létezik, mivel semmi sem lehet egyszerre hideg és forró, csakhogy a piszkavas egyszer hideg, máskor forró, tehát hideg is meg meleg is, ami lehetetlen, ergo nem létezik. Ugyanez másképp: semmi sem lehet a „múlt, jelen, jövő” tulajdonságai közül kettő egyszerre. Ámde minden időpont jövő is, majd jelen, végül múlt, következésképpen az idő ellentmondásos, tehát nem létezik. – á la McTaggart.)
Matematikai alapok
Vajon pusztán logikai-halmazelméleti eszközökkel mit tudunk kifejezni az idő természetéből? Célszerű ehhez egy reláció formális tulajdonságait megvizsgálni. Legyen ’≤’ reláció három axiómával jellemzett:
1: reflexív (minden x-re x≤x)
2: tranzitív (ha x≤y és y≤z akkor x≤z)
3: antiszimmetrikus (ha x≤y és y≤x akkor x=y).
Tetszőleges halmazon ilyen formális tulajdonságokkal rendelkező relációt a matematikában 'parciális rendezés'-nek nevezik. Ha valamely T alaphalmazon – melyet a rendezés értelmezési tartományának is szoktak nevezni – bármely két x,y elemre teljesül, hogy x≤y vagy y≤x, akkor azt mondjuk, hogy a rendezés teljes. Szokták ezt lineáris rendezésnek vagy láncnak is nevezni. Azt mondjuk, hogy valamely u elem minimális, ha nincs olyan tőle különböző y elem, amelyre y≤u. Ha T halmazon a rendezés teljes, akkor legfeljebb egyetlen minimális elem van, amit a legkisebb elemnek nevezünk. Hasonlóképpen értelmezhető a maximális és a legnagyobb elem is. A rendezés irreflexív változatát ’szigorú rendezés’-nek nevezik, melynek szokásosan ’<’ a jelölése. Az ilyen „x korábbi mint y” aszimmetrikus reláción alapuló szigorú rendezést nevezte McTaggart B sorozatnak.
Az idő valamiknek (nevezzük ezeket időpontoknak) a parciálisan rendezett T halmaza. A T halmazok lokálisak abban az értelemben, hogy merev testekhez kötötten adottak. Egy adott merev test és időskála esetén a <T,R> parciális rendezés teljes – azaz a T halmaz bármely két x,y eleme között fennáll xRy vagy yRx. Azt nem feltételezzük, hogy a lokális idő halmazok egyesítése esetén is bármely két elem (időpont) összehasonlítható, nem tesszük föl tehát, hogy van világidő. Nem kell döntenünk abban a kérdésben sem, hogy az idő folytonos-e vagy diszkrét, van-e kezdeti időpont, és egyirányú-e vagy körben forog az idő. Ezek ugyanis jól definiálhatóak formális fogalmakkal, a relációra vonatkozó kikötésekkel.
Ha T teljesen rendezett halmaz ám nincs benne sem legkisebb sem legnagyobb elem, akkor T egy végtelen időskálának tekinthető. Ki tudjuk tehát fejezni az időskálák rendezett jellegét, a méretét, hogy véges, vagy végtelen, és további eszközökkel, még a sűrűségét is, tehát, hogy az idő folytonos, vagy diszkrét. Viszont az időt egyszerűen órák állapotsorozataként fölfogva, pusztán formális kritériumokkal nem tudjuk megkülönböztetni a múltba vagy a jövő felé mutató irányt, és azt sem tudjuk kifejezni, hogy az idő múlik.
A jelenlét talánya
Nem tudjuk kifejezni a matematikai fizika nyelvén a következőket.
- Mindig a jelenben élünk, mindig a jelenben létezünk. Úgy tűnik a fizikai tárgyak létezése jelen idejű.
- Az idő megállíthatatlanul múlik, a jelen csak egy pillanat, bár a változás mértékét befolyásolhatják fizikai tények.
- A múlt már nem létezik és a jövő még nem létezik.
- A fizikai tárgyak változhatnak, de egy múltbeli esemény megváltoztathatatlan.
Ezek az összefüggések azért nem fejezhetőek ki fizikai egyenletekkel, mert a matematikai formulák a statikus szöveg időtlen világában léteznek. Az egzisztenciális kvantor nem a jelenre vonatkozik, ha pl. egy halmaz eleme egy másik halmaznak, az nem időbeli viszony, hanem időn kívüli, örök kapcsolat. A kibertérben megszűnik ez a korlát, mert a kibertér maga időbeli. A kibertérben egy változó adott időpontban kap értéket, és ez az érték változhat az időben. A kibertérben egy változó értékadása indexikus kifejezésként értelmezhető.
Nem mindegy, hogy miknek a halmazán értelmezzük a „korábbi vagy egyidejű” relációt. Események halmazának egyidejű események is elemei lehetnek. Legyen két ilyen különböző esemény mondjuk e1 és e2. Tehát e1¹e2. Ekkor azonban mivel mindkét esemény egyidejű, e1≤e2 és e2≤e1 egyaránt fönnáll, miből ’≤’ reláció antiszimmetrikus mivolta miatt e1=e2 következik, csakhogy ez ellentmondás. A tanulság ebből az, hogy a ’≤’ – azaz a ’korábbi vagy egyidejű reláció – nem értelmezhető általában az események halmazán, hanem csak egyedi események idő adatai halmazán. Az egyidejű eseményeknek azonos idő adataik vannak. Tulajdonképpen az idő adatok is egyfajta események. Némelyik idealizált egyedi esemény halmazt órának nevezzük. Az idő értelmezéséhez az órákon kívül még az egyidejűség relációjára is szükségünk van. Az egyidejűség relációja egy leképezést jelent az események halmazából az óra állapotainak halmazába, ahol egyidejűnek tekintendők azon események, melyek képe megegyezik. Tévedés tehát az a filozófusok körében gyakori vélekedés, hogy az idő egyszerűen egy „korábbi vagy egyidejű” (vagy későbbi) reláció az események halmazán. Valójában az idő az órák „korábbi vagy egyidejű” relációja értelmezési tartományába való leképezése az események valamely halmazának. Az idő tehát relációk relációja. A következőkben megmutatom, hogy az múltra, jelentre és jövőre vonatkozó indexikus kifejezések a nyomtatott szöveg statikus világában egy időskála értelmezési tartományán értelmezett relációként is értelmezhetőek.
Egy biztos állítás
Minden normális éber személy, amikor kimondja, hogy „Én most itt vagyok.”, akkor tévedhetetlenül igazat mond. Az igazság ebben az esetben a mondat által kifejezett propozícióra, és nem a mondatra vonatkozik, mert magának a mondatnak nincs igazságértéke. Ezzel szemben a mondat által adott összefüggésben kifejezett propozíciónak van igazságértéke, amely időtlen. Azért nincs a mondatnak önmagában igazságértéke, mert olyan logikai alkatrészeket tartalmaz melyek extenziója meghatározatlan. Az „Én most itt vagyok.” mondat ugyanis sajátos logikai-grammatikai összetevőket – indexikus kifejezéseket tartalmaz – melyeknek csak a megnyilatkozás összefüggésében van egyértelmű referenciája. Az „én”, „most”, „itt” szavak jelentésének épp a bizonytalanság a lényege, az a különös, ám nélkülözhetetlen szerep, hogy helyzetről-helyzetre változtatják azt, amire utalnak, amit jelölnek.
Tegyük fel, hogy ezt a mondatot N.N. úr mondja t1 időpontban h1 helyen. Ekkor kicserélve az indexikusokat nevekre a következő mondatot kapjuk: N.N. úr t1 időpontban h1 helyen tartózkodik. Ez már egy logikailag perfekt mondat, logikai-grammatikai alkatrészei egyértelmű extenzióval bírnak. Az „N.N. úr” név egy személyre, „t1 időpont” egy időpontra, „h1 helye” egy helyre referál. Figyeljük meg, hogy ez utóbbi mondat már lehet igaz vagy hamis, attól függően, hogy fennáll-e egy tény vagy sem. Szemben a propozíciókkal, a perfekt mondatok bár ritkák a mindennapi nyelvhasználatban, de evilági dolgok, mondatok, melyek előfordulhatnak az írásbeli kommunikáció terében. Ezzel szemben a propozíciók, az indexikus kifejezéseket tartalmazó mondatok feltételezett igazsághordozói, időn és téren kívül léteznek, nem pusztán nyomtatott vagy elektronikus jelsorozatai valamely nyelvnek.
Foglaljuk össze az eddigieket:
Van egy esemény:
e1: = N.N. úr t1 időpontban h1 helyen azt mondja, „Én most itt vagyok.”
Egy igaz vagy hamis információt kifejezni szándékozó (konstatív) indexikus mondat:
s1:= Én most itt vagyok.
Egy perfekt mondat:
s2:= N.N. úr t1 időpontban h1 helyen tartózkodik.
Egy propozíció:
p1:= az a tény ami igazzá teszi s2 mondatot.
Miért igaz mindig az s1 indexikus mondat kifejezte propozíció? Azért, mert bármely x személy, bármely y időpontban, bármely z helyen kimondja, a mondat indexikus alkatrészei az esemény ezen összetevőire fognak mutatni, automatikusan létrehozva a mondat által kifejezett propozíciót igazoló eseményt, a propozíció igazság hordozóját (truthmakerjét).
Vannak olyan indexikus kifejezést tartalmazó mondatok is, melyeknek nem fejeznek ki propozíciót, vagy csak mellékesen teszik azt. Ezek a mondatok nem, vagy elsősorban nem tényállást szándékoznak közölni, hanem bejelentenek, figyelmeztetnek, jeleznek, vagy éppen óhajtanak. Azzal a mondattal, hogy „Most értünk oda.” jelezzük, hogy célba értünk. Ebben a mondatban nem cserélhető föl az indexikus „most” kifejezés egy adott időponttal a jelentés lényegi megváltozása nélkül. Abban a mondatban, hogy „Ez Ali baba háza.” szintén nem cserélhető föl az indexikus „ez” kifejezés a ház GPS koordinátáival, különösen, ha olyankor hangzik el, amikor még nem találták fel ezt a fajta helymeghatározást.
Más konstatív indexikus mondatok a tényektől függően igazak vagy hamisak. Az „A piszkavas forró volt, de most már kihűlt.” mondat igaz, ha létezik a piszkavas és:
- van olyan a mondat kimondását megelőző t időpont, hogy a piszkavas forró t-kor.
- a mondat kimondásával azonos j időpontban a piszkavas hideg.
Magának az indexikus kifejezést tartalmazó mondatnak most sincs igazságértéke csak az általa kifejezett propozíciónak, és a propozíció igazságértéke most is örök változatlan. Ennek semmilyen módon nem mond ellent az a különös feltevés, hogy a piszkavas valamikori forróságát igazoló esemény a t időpont előtt a jövőhöz tartozott, aztán jelenné lett t időpontban, majd később pedig múlt részévé vált. Ugyanis nem a propozíciók igazságértéke változik – ami lehetetlen – hanem az események idejének a mindenkori jelenhez való viszonya.
Ezzel elérkeztünk vizsgálódásunk egy sarkalatos pontjához: ha az olvasó ezt a szöveget nyomtatott formában olvassa, akkor a szöveg megjelenései között nem fordulhatnak elő események, mert a nyomtatott szöveg statikus. Ebből következik, hogy amikor az imént e1 eseményről beszéltem, maga az esemény nem fordulhat elő a holt szöveg közegében, csak a neve; ezzel szemben s1 és s2 mondat valóban ott van a papíron. Megváltozik a helyzet, ha az olvasó ezt a szöveget a kibertérben olvassa. Ott elfordulhatnak események is, melyek hatására egy elektronikus karaktersorozat más és más állapotokba kerülhet, és ott megjelenhet az idő.
Egyszerű példa
Képzeljük el, hogy N.N. úr egy piciny egydimenziós véges világ lakója, amelyik mindössze tizenkét helyből és időpontból áll. N.N. úr élete semmi másból nem áll, mint a tizenkét helyen való folyamatos haladásból. Történetesen ebben a világban az idő körbe jár, de ez nem mond ellent a múlt változtathatatlanságának és az igazságértékek állandóságának, mert ebben a világban minden időpontban mindig ugyanaz történik. Az időpontokat és a helyeket is az egyszerűség kedvéért számokkal jelöltem. Alább egy N.N. úr világáról készült pillanatfelvétel látható, ő éppen a negyedik helyen tartózkodik t4 időpontban (1.táblázat):
1. táblázat
|
|
|
|
N.N. |
|
|
|
|
|
|
|
|
Az összes időponthoz tartozó hely relációját (grafikonját) így ábrázolhatjuk (1. ábra):
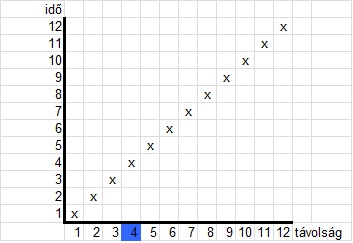 1. ábra
1. ábra
Mennyit mutat meg ez a grafikon az idő természetéből?
Az „Én most itt vagyok.” mondatot nyilván soha senki nem mondja ki komoly szándékkal, hiszen mivel mindig igaz, nincs információ tartalma, de más hasonló mondatokat annál inkább. A mondatban szereplő első indexikus kifejezés egy személyre, a második kettő pedig a tér-idő valamely tartományára vonatkozik. Első típust, az „én”-t tartalmazó némelyik rejtélyes mondat – (én) gondolkodom – Descartes óta véget nem érő filozófiai viták tárgya, a második, a tér-időre vonatkozó indexikusok pedig McTaggart klasszikus, az idő realitását tagadó gondolatmenete óta tárgya vég nélküli vitáknak.[vi] McTaggart éles elméjűen észrevette, hogy az „itt” és „most” indexikus kifejezések között van egy lényeges különbség: N.N. úr megteheti, hogy helyben marad, és akkor két egymást követő időpontban az „itt” ugyanazt a helyet fogja jelölni, N.N. úr megállíthatja a térbeli változást. Ezzel szemben N.N. úr hiába szólna a pillanathoz, „oly szép vagy, ó, maradj tovább!”, nem állíthatja meg az időt – legalábbis a klasszikus fizika világában biztosan nem.[vii] A „most” jelentése szükségszerűen megváltozik minden időpillanattal és ezt a fenti reláció nem ábrázolja. A fenti grafikont a kibertérbe áthelyezve láthatjuk, hogy N.N. úr helye a grafikonnak megfelelően változik, de miképp ábrázolható a jelen folyamatos változása időtlenül egy reláció segítségével? Miképp ábrázolható ellentmondásmentesen az időtlen, statikus nyelv világában az, hogy a jövőbeli időpontok előbb jelenné, majd múlttá válnak? Mind a valóság, a mindennapi lét, mind a leírás, az igazság dimenzióját mutatja az alábbi Excel modell:
http://ferenc.andrasek.hu/modellek/time-series-hu.xlsx
Az A sorozat definíciója a B sorozat alapján
McTaggart A sorozaton az idő „jövő, jelen, múlt” indexikus tulajdonságainak sorozatát, B sorozaton az időpontok rendezett sorozatát, C sorozaton pedig egyszerűen rendezést ért. A B sorozat általa adott értelmezésétől annyiban eltérek, hogy nem a „korábbi” hanem a „korábbi vagy egyidejű” antiszimmetrikus reláció alapján értelmezem, mert így egyszerűbb.
Az alábbi ábrán N.N. úr a negyedik időpontban van jelen (2. ábra):
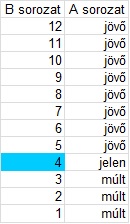 2. ábra
2. ábra
A következő időpontban az 5. időpontba kerül (3. ábra):
 3. ábra
3. ábra
Olyan az A sorozat viszonya a B sorozathoz, mint a zenében a szolmizálás viszonya az abszolút zenei hangok kottázásához. Az utóbbiból levezethető az előbbi, de fordítva nem igaz. A „múlt, jelen, jövő” nem ad eléggé részletes felbontást, de finomíthatjuk az idő relatív skáláját a „régmúlt, múlt, közelmúlt, az imént” valamint a „nemsokára, mindjárt, közeljövőben, jövőben, távoli jövőben” fogalmak alkalmazásával. Még ennél is tovább mehetünk, ha végtelen sok elemre van szükségünk. Jelöljük 0-val a jelent, -1 el az „imént”-et, -2 vel a közelmúltat, stb. és hasonlóképpen 1-el a „nemsokára”-t, 2-vel a „közeljövő”-t stb. A későbbiekben mind az A sorozat elemeit, mind a B sorozat elemeit számokkal ábrázolom, de az utóbbiakat a vízszintes tengelyeken, míg az előbbit a függőleges tengelyen.
Az A-sorozat meghatározását keresve előbb be kell lássuk, hogy valamennyi fizikai tárgy valamennyi mérhető tulajdonsága tér-időhöz kötött, hiszen képtelenség téren és időn kívül mérést végezni. Mivel az idő maga is mérhető fizikai tulajdonság, így az idő is téridőhöz kötött, és azért az idő azon tulajdonsága, hogy jövőből jelenné, majd múlttá válik, maga is időben értelmezett. Ábrázoljuk ezt a relációt N.N. úr világában!
Legyen adott az időpontok halmaza, melyet az ismertetett módon egész számokkal ábrázolok:
Legyenek x,y elemek az idő B sorozata halmaza elemei.
y x-hoz képes jövő idejű akkor és csak akkor ha y-x>0
y x-hoz képes jelen idejű akkor és csak akkor ha y-x=0
y x-hoz képes múlt idejű akkor és csak akkor ha y-x<0
Ez alapján az idő önmagára vonatkoztatott következő relációját kapjuk (4.ábra):
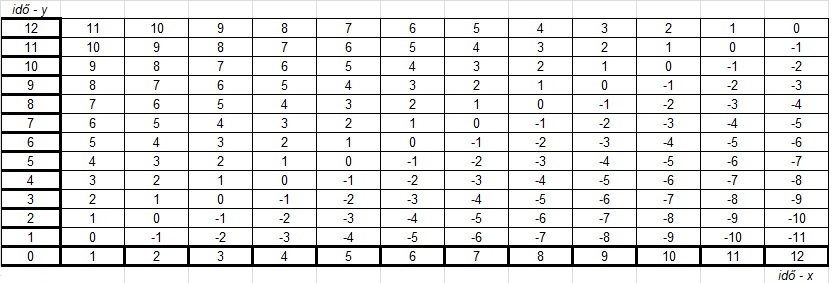 4. ábra
4. ábra
A táblázatot grafikusan ábrázolva láthatjuk, hogy a jelen először az 1., majd a 2. időpontba kerül, kérlelhetetlenül halad előre a benne utazóval, miközben a jövő vízesésszerűen a jelenbe zuhan, majd örökre alászáll a múltba. (5.ábra)
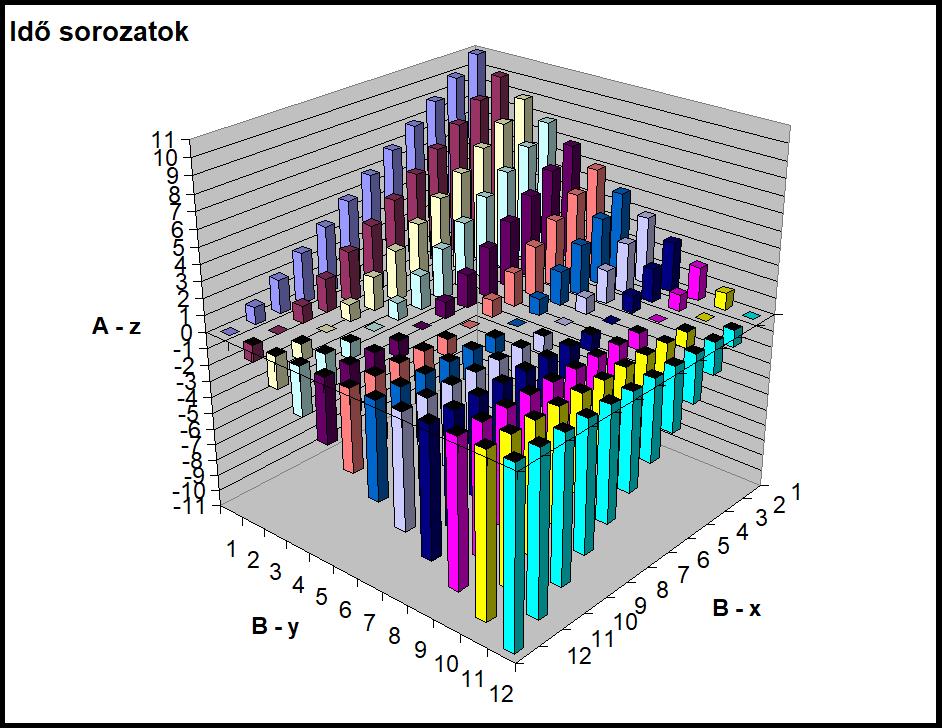
Az időpontok tartományán alkalmazva az alábbi rövidítést – x £ y akkor és csak akkor ha x korábbi vagy egyidejű y-al – belátható, hogy:
y x-hez képest jövő pontosan akkor ha x≤y és nem y≤x
y x-hez képest jelen pontosan akkor ha x≤y és y≤x
y x-hez képest múlt pontosan akkor ha y≤x és nem x≤y
Az A sorozat egyszerűsített felfogását alkalmazva az alábbi táblázatot kapjuk (6.ábra):
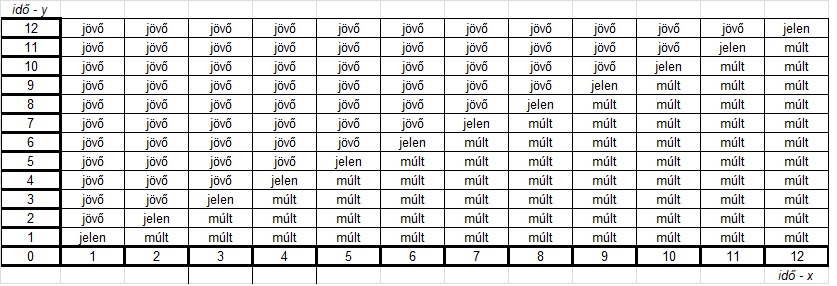 6. ábra
6. ábra
Figyeljük meg, hogy 1. időpontban a 2. és 3. időpont még jövő, miközben a 2. időpontban az 1. már a múlt része, 2. a jelen, és 3. továbbra is jövő. A reláció grafikonján – a táblázatban – a jelen fokozatosan emelkedik az egyre nagyon számok irányába. Ez megfelel McTaggart belátásának, miszerint az A sorozat a múltból a jövő felé halad. A kibertérben a valóságban is látszik az idő múlása, amire a statikus szöveg mégoly spekulatív filozófiai nyelvet használva sem képes. Az A sorozat tehát definiálható a B sorozat segítségével, így az előbbi valóságosságát megalapozza az utóbbi valóságossága.
Mi változik az időben?
Nevezzük valaminek a hőmérsékletét ’fizikai-jellemző’-nek. A jellemzők olyan funktorok, melyek hiányzó helyein individuum nevek szerepelhetnek, és az üres helyeket megengedett módon kitöltve szintén individuum nevet kapunk. Másképp fogalmazva a jellemzők terjedelmei függvények. Ezek alapján a ’piszkavas hőmérséklete’ egy függvény, amely a piszkavashoz egy bizonyos időpontban – mondjuk t2 kor – a „forró“ míg egy másik időpontban – mondjuk t1 kor – a „hideg“ állapotot rendeli. A függvény összetartozó (állapot, időpont) rendezett párjait ’esemény’-nek nevezzük. Amit az eseményekre való hivatkozással fejezünk ki, azt kifejezhetjük mondatokkal is ilyen módon:
hideg=hőmérséklete(piszkavas, t1) és forró=hőmérséklete(piszkavas, t2)
Ez utóbbi beszédmódot képviseli a tényekre való hivatkozást, mivel itt ’mondat’ típusú kifejezéseket használunk ugyanazon valamiknek a leírására, amikre korábban megnevezésekkel utaltunk, az ’esemény’ szó használatával. A változás abban áll, hogy:
hőmérséklete(piszkavas, t1) ≠ hőmérséklete(piszkavas, t2)
Ezt a megközelítést azonban McTaggart nem fogadja el, mert szerinte: „Ez azonban nem okoz változást a piszkavas tulajdonságaiban. Ez a piszkavas mindig rendelkezik azzal a tulajdonsággal, hogy forró azon a bizonyos napon; ugyanakkor azzal a tulajdonsággal is, hogy nem forró egyetlen más időpontban sem. Mindkét tulajdonsággal rendelkezik minden időpontban – akkor is, amikor forró, akkor is, amikor hideg. Ezért úgy tűnik, helytelen azt mondani, hogy a piszkavas változik. A tény, hogy a piszkavas egy sorozat egyik pontján forró, és más pontjaiban hideg, nem jelenthet változást, ha ezen tények egyike sem változik – márpedig egyik sem változik. Nem változik a piszkavassal kapcsolatos többi tény sem, hacsak nem változik a piszkavas jelen, múlt vagy jövőbelisége.“
McTaggart sajátos módon értelmezi a tulajdonságot, de más felfogások is lehetségesek. Ezek kifejezéséhez felhasználok egy formális logikai technikát. A ’λxf(x)’ kifejezés, feltéve hogy x változó U halmazon értelmezett, minden U-beli u elemhez hozzárendeli az f(u) függvényértéket, röviden az ’f’ függvény értékmenetét adja meg. Tehát pl.: a ’λx.x2’ formula a számok és négyzeteikből álló párok halmazát határozza meg. Ezek alapján az egyes filozófiai ’tulajdonság’ felfogások így fejezhetők ki:
McTaggart: λx (x forró azon a bizonyos napon) – ekkor nincs változás a Russelli értelemben
Russell: λx λt (x forró t napon) – ekkor van változás.
Vagy tulajdonságok helyett a ’jellemzők’ fogalmában gondolkozva:
λx λt forró=hőmérséklete(x,t) – ekkor is van változás
Tanulságos McTaggart következő példája is. „Vizsgáljunk meg egy másfajta sorozatot. A greenwichi meridián szélességi fokok sorozatát szeli át. Találhatunk két pontot ebben a sorozatban, mondjuk S-et és S'-t, amelyekre igaz az a propozíció, hogy „S-nél a greenwichi meridián az Egyesült Királyságon belül van”, míg hamis az a propozíció, hogy „S'-nél a greenwichi meridián az Egyesült Királyságon belül van”. Mégsem mondaná azt senki, hogy ez változást jelent. Miért mondanánk akkor ezt a másik sorozat esetében?“
Miért ne mondaná? S-nél a greenwichi meridián más viszonyban van az Egyesült Királyság térbeli helyével mint S'-nél. Ha S'-hez érkezünk, megváltozik a greenwichi meridián hozzánk képesti térbeli viszonya.
Russell megközelítése a változás fogalmáról a modern tudomány személetmódja. Ha Russell felfogása elfogadhatatlan, akkor semmit sem magyaráz meg a Galilei utáni matematikai fizika, semmit a matematikai analízis alkalmazása a fizikai világ jelenségeire, akkor az egész modern természettudomány hajítófát sem ér.
Au revoir
Végezetül egy mondatban összefoglalható az a filozófiai perspektíva amit védelmezni kívántam: az idő az írott szöveg statikus világában, azaz az igazság időn kívüli ontológiai dimenziójában úgy írható le, mint relációk relációja, az idő létezik, és fogalma nem ellentmondásos.[i]
Innen letölthető: http://ferenc.andrasek.hu/pdf-papers/time/a-jelenlet-talanya4.pdf
[i] Javasolt irodalom: Tim Crane – Katalin Farkas (eds.) (2004) Metaphysics, A Guide and Anthology, Oxford: Oxford University Press c. könyvében föllelhető McTaggart klasszikus tanulmányán kívül Arthur N. Prior: Changes in events and changes in things című írása, Paul Horwich egy könyv részlete a ’moving now’koncepcióról valamint J.J.C.Smart-nak a négydimenziótér-idő realitását védelmező álláspontja. Érdemes elolvasni Nyíri Kristóf: Hundred Years After: How McTaggart Became a Thing of the Past c. dolgozatát (http://www.hunfi.hu/nyiri/Nyiri_ECAP_2008.pdf). Huoranszky Ferenc, Modern Metafizika, (2001) Osiris kiadó, Bp. c. könyve V. fejezetében foglalkozik az idő problémájával az enyémtől némileg eltérő megközelítéssel. http://www.tankonyvtar.hu/filozofia/modern-metafizika-080905-3.
[i] Sean Carroll, Most vagy mindörökké (From eternity to here. The quest for ultimate theory of time) (2010) Akadémiai kiadó, Bp. p.22,23
[ii] Miért az, mi lenne, ha megváltozhatna? Képzeljük egy, hogy egy bizonyos napon délután sétálni mentem. Így igaz az arra a délutáni sétára vonatkozó p kijelentésem. Később azonban visszamegyek az időben, és azon a napon nem sétálok, hanem otthon ülök a karosszékben és olvasok. Ekkor hamis az arra a délutáni sétára vonatkozó p kijelentésem. Egy még későbbi időpontban azonban arra az időpontra térek vissza, amikor visszatértem a múltba és séta helyett üldögéltem. Ezen második visszatérésemmel semmivé teszem az első időutazásomat, és így újra igaz p, azaz, hogy azon a bizonyos napon sétálni mentem. Egy még későbbi időpont azonban, a második időutazást annihilálja, és föltámasztja az elsőt, minek következtében, mégsem sétáltam azon a napon, tehát p hamis. És ez így folytatódhat vég nélkül, sosem lehetünk biztosak abban, hogy sétáltam akkor vagy sem, azaz sosem lehetünk biztosak p igazságában. És ez nem a legrosszabb lehetőség. Tegyük fel, hogy két különböző jövőbeli pillanatból térek vissza ama délutánra, amikor sétálni indultam. A két különböző időbeli visszatérés két különböző módon változtatja meg a múltat. Az első sétálás helyett múzeumlátogatásra vezet, míg a másik, hangverseny látogatásra. Ekkor azonban nem tudjuk, hogyan változott meg a múlt, sétálás helyett múzeumba mentem vagy hangversenyre? Mindez teljes zűrzavart okozna, hiszen ez a bizonytalanság számtalan más kijelentés esetén is fönnállna ezen a módon. A múlt megváltoztatása tehát értelmetlenséghez vezetne, ezért a feltételezését elvetjük.
[iii] A sziget a Duna Vaskapu-szorosban volt, a 70-es években a jugoszláv-román vízerőmű megépítésekor teljesen víz alá került, állítólag ihletül szolgált Jókai Mór, Az arany ember című regényében szereplő Senki szigetéhez.
http://www.origo.hu/nagyvilag/20070817-milliokat-telepitenek-ki-a-vizeromuvek-es-gatak-epitese-miatt.html?pIdx=1
[iv] Quine szerint a létezés mindhárom esetben ugyanazt jelenti, pusztán arról van szó, hogy más-más fajta dolgok létezéséről beszélünk. Tehát szerinte a különbség nem a létezés fogalmában van az egyes esetekben, hanem a tárgyában, abban, aminek a létezéséről szó van.
[v] Azért ingoványos, mert a tapasztalatok általában vett megbízhatatlanságát alátámasztó érveknek maguknak is tapasztalatokra kell hivatkozniuk. Utóbbiaknak megbízhatóaknak kell lenniük, különben az érv maga is megbízhatatlan alapokon nyugszik. Ebből viszont az következi, hogy nem lehet minden tapasztalat megbízhatatlan.
[vi] John McTaggart: „Time”. The Nature of Existence (Cambridge: Cambridge University Press, 1927), 33. fejezet, ford.Csordás Attila. in.: Farkas Katalin-Huoranszki Ferenc (szerk.): Modern Metafizikai Tanulmányok ELTE Eötvös Kiadó, Budapest 2004. A fordítás elektronikusan is hozzáférhető: http://www.szv.hu ezért nem adok meg oldalszámokat. Prof. Soshichi Uchii így foglalja össze McTaggart gondolatmenetét: „Let me summarize McTaggart's argument as I understand, by the following figure. The 'moving now' generates an A series, and hence a B series, out of a permanent C series. And since changes generated by this A series are supposed to be a part of reality, temporal facts, such as 'E is present', must also belong to reality; these requirements lead to a contradiction.” http://www.bun.kyoto-u.ac.jp/~suchii/mctaggart.html
[vii] Goethe, Faust (ford. Csorba Győző) (1961) Magyar Helikon, Bp., II. köt. p. 393.