Előhang
Valamikor a 80-as évek közepén fogalmaztam meg először az alábbi gondolatokat, de később többször elvetettem, majd módosított formában újra és újra elő vettem azokat. Most sem vagyok biztos ezek helyességében, de az alábbi problémák és ahhoz kapcsolódó fogalmak több korábbi írásomban is szerepelnek, így az alábbi szöveg arra mindenképpen jó, hogy világosabbá tegye mire gondoltam, amikor a létezés dimenzióiról beszéltem.
Probléma felvetés
Az idő filozófiájának jelenkori fókuszában az a kérdés áll, hogy az idő A vagy B elmélete a helyes, melyik írja le helyesen az idő természetét, azaz a valóságot? Úgy tűnik, ha kizárólag az időbeli viszonyokat ábrázoló B elmélet a helyes, akkor a ’jelen’ fogalma pszichológiai kérdés, a jelenben való lét sokkal inkább az emberi természet jellemzője, mint a fizikai valóságé; ha viszont az idő A teóriája az idő adekvát elmélete, akkor az időt a téridő egyik koordinátájaként, azaz mérhető fizikai jellemzőként értelmező B teória hibás, mert hiányos, az idő lényeges tulajdonságairól hallgat.
Miért gondolja sok fizikus és filozófus, hogy az idő B elmélete a helyes, és bármely időpontban történt esemény létezik -- a létezésnek a logika egzisztenciális kvantor által kifejezett időtlen értelmében -- csak némelyikre hatással lehetünk, másokra meg nem? (A hatások véges terjedési sebessége miatt nem csak a múltra, de a tőlünk távolabb lévő jelenre sem lehetünk befolyással.) Ennek a tévedésnek az az oka, hogy az idő ábrázolása, a matematikai-geometriai modell, ahogy a tudományban megjelenik, természetessé vált, része a köznapi szemléletnek, megtanuljuk az iskolában. Ennek következtében sokan a modell sajátos tulajdonságait a valóság tulajdonságának tulajdonítják. A bolygók mozgását ábrázoló grafikonok, vagy világvonalak a Minkowski téridőben valóban egyszerre ábrázolják az időpontokat, a jelen vagy a múlt csak egy viszony ebben a modellben. A grafikonon tényleg egyszerre ott van minden időpont, és ezt megszoktuk, természetesnek tartjuk. Természetesnek tartjuk az idő geometrizálását, ezért sokan tartják értelmesnek a kérdést, hogy miért nem mehetünk vissza az időben. Holott a kérdés értelmetlen. Az idő éppenséggel folyhatna visszafelé, de a múlt akkor sem változtatható meg. A fizikának erre a geometriai szemléletre van szüksége, a „múlt, jelen, jövő” fogalmai csak így, relációként értelmezhetőek ebben a matematikai-geometriai modellben. A modell azonban nem azonos azzal, amit modellál, nem azonos a valósággal. Valójában a jelenben élünk, és minden tárgy is a saját jelenében létezik. Ezek a jelenek lehetnek vonatkoztatási rendszerfüggőek más nézőpontból, a tárgyakat helyezve az origóba, azonban abszolút jellegűek. A múlt, jelen és jövő fogalmai jelentését nem tudja kifejezni a fizika az ő matematikai nyelvén.
Az idő mind az A mind a B elméletének meg van a létjogosultsága. Azt szeretném bemutatni, hogy a két felfogás összekapcsolható egyetlen ontológiában, ahol mindkét szemlélet érvényesül, nem tagadják, hanem kiegészítik egymást. A lét ugyanis kétdimenziós: egyrészt időbeli dimenzió (nevezhetjük a mindennapi lét dimenziójának), másrészt az igazság, (vagy a tudomány) dimenziója.
Golyó gurul az asztalon
Vessük össze az alábbi két mondatot a ténybeli igazság szempontjából:
(1) 2018. augusztus elsején délben egy golyó gurult végig egy vonal mentén, az asztalon.
(2) Most, 2018. augusztus elsején délben egy golyó gurult végig egy vonal mentén, az asztalon.
Történetesen most, amikor e sorokat írom mindkét mondat igaz, de később, amikor ezt a mondatot olvassa valaki, megváltozik a helyzet. Az (1) mondat továbbra is igaz marad, igaz volt korábban is – bár nem tudtuk előre, hogy most mi fog történni – igaz most, és igaz marad későbben is, igazságértéke örök, változatlan. A második mondat többet állít. A második mondat nem csak egy jól meghatározott e1 eseményt állít egy meghatározott időben, hanem azt is állítja, hogy éppen most történik az e1 esemény. Ha holnap ugyanez a golyó, ugyanazon az asztalon, ugyanúgy végig gurul, az egy másik esemény lesz, nem lesz azonos a mostanival. Nevezzük ezt a későbbi eseményt e2-nek. Miért nem azonos e1 és e2? Azért nem azonos, mert az első 2018. augusztus elsején délben, míg a második egy nappal később, 2018. augusztus másodikán délben történt. Az e1 esemény megtörtént, és soha többé nem történhet meg, befolyásolni sem tudjuk utólag semmilyen módon. Az e1 esemény megtörtént, és lehetetlen meg nem történtté tenni. Azért van az így, mert a múltba süllyedt, és semmilyen módon nem tudunk hatással lenni a múltra. (Az időben való esetleges visszafelé haladás sem mond ennek ellent, az mást jelent.)
A (2) mondat, hogy a golyó most, ma délben végig gurult az asztalon nem volt igaz korábban, és nem lesz soha későbben sem igaz, csak megfogalmazása idején, akkor, amikor a mondat megfogalmazása történt. Bontsuk két részre a második mondatot:
(2.1) 2018. augusztus elsején délben egy golyó gurult végig egy vonal mentén, az asztalon.
(2.2) Most 2018. augusztus elseje dél van.
Próbáljuk meg formális logikai nyelven kifejezni a gondolatot. Vezessük be a következő jelöléseket:
t1:= 2018. augusztus elseje dél
m:= most
E(x,t):= x golyó végig gurult egy vonal mentén, az asztalon t időszakban.
Ezek alapján a korábbi két mondat egy kézenfekvő formalizálása a klasszikus logika nyelvén a következő:
(3.1) E(x,t1)
(2018. augusztus délben x golyó végig gurult egy vonal mentén, az asztalon)
(3.2) m = t1
(Most 2018. augusztus elseje dél van.)
A korábbi (2) mondat tehát azt állítja, hogy most, 2018. augusztus elseje délben egy golyó végig gurult egy vonal mentén, az asztalon. Ugyanez a gondolat formális nyelven megfogalmazva:
(4) E(x,t1) & m = t1
Lambda operátor alkalmazásával megkísérelhetjük kihangsúlyozni a mondat jelenre való utalását, ahol x=egy adott golyó:
(5) λz λy (E(x,z) & z=y) (t1)(m)
(Most egy golyó gurult végig az asztalon.)
A jelen ilyen módon való kifejezése formális logikai nyelven azonban vitatható. A klasszikus logika formuláinak szemantikai interpretációjában az individuum nevek – jelen esetben ’m’ – az értelmezési tartomány egy és csak egy elemét jelölik. Amennyiben az értelmezési tartomány időpontokat is tartalmaz, akkor annak egy elemét is jelölhetik, de nem képesek a mindenkori jelent, a ’most’-ot jelölni. Úgy tűnik (2) kifejezése a klasszikus logika formalizált nyelvének standard interpretációjában lehetetlen. Valójában azért van ez így, mert az írás, a nyomtatott szöveg világa statikus, a jelek nem mozdulnak meg a papíron. Ezzel szemben a számítógép, vagy automaták nyelvén mindez könnyen ábrázolható. Legyen a számítógép vagy az automata beépített órájának értéke azonos ’m’ változó értékével. Ekkor a program nyelven az ’m = 2018.08.01.12:00’ formula igaz lesz azon a bizonyos napon, és hamis máskor. Az automaták világában, a kibertérben tehát kifejezhető a mindenkori jelenre való utalás. Tehát a korábbi (2) köznyelvi mondat, amelyet minden kompetens fölhasználó megért, hogy „Most egy golyó gurult végig az asztalon.”, könnyedén kifejezhető valamilyen programozási nyelven, és megjeleníthető a kibertérben, míg a formális logika nyelvén nem, vagy csak az interpretáció szabályainak megsértésével.
A nyelv alapvető célja nem az igazságok gyűjtögetése, hanem a cselekvés. Az ismeretérték a ’tedd ezt ha igaz, és amazt ha hamis’ feltételes utasítás esetén bír jelentőséggel a való életben. Hasonló ez a programozási nyelvek feltételes utasításaihoz, melyek szintén egy megítélhető tartalmú mondat igazságától teszik függővé, hogy merre fusson tovább, mit tegyen a számítógép program. Ebből a nézőpontból a programozási nyelvek teljesebben tükrözik az ember és világa kapcsolatát mind a szimbolikus logikai nyelvek. Ezt a lehetőséget használja a ki a következő modell.
Gondolatkísérlet helyett működő modell
A kortárs analitikus filozófiában gyakori a gondolati kísérlettel alátámasztott érvelés. Én modelleket használok filozófiai álláspontom alátámasztására, melyek némileg hasonlatosak a gondolati kísérletekhez. A kortárs analitikus filozófiában a gondolati kísérlet magyarázataiként többnyire természetes nyelvi megfogalmazások szerepelnek. Ezzel szemben én a modellek leírásakor a (részben) logikai-matematikai nyelvet részesítem előnyben. A formális nyelven megfogalmazott modellekhez sok esetben működő táblázatkezelő modelleket csatolok, melyek olyan összefüggéseket is képesek bemutatni, melyekre a statikus természetes vagy formális nyelv képtelen. Ilyen módon modellekkel ábrázoltam szemantikai paradoxonokat és az igazság fogalmának egyfajta értelmezését, az idő filozófiájával kapcsolatos kérdéseket, az oksággal és a determinizmus fogalmával kérdéseket, Wittgenstein piszkavasát, rugókat és Thészeusz hajóját. Mindezek a modellek puszta létükkel megoldást kínálnak számos filozófiai rejtélyre. Ugyanis ha egy gondolatnak van működő modellje, akkor az nem lehet ellentmondásos, az ellentmondásosságát állító filozófiai érvelés hibás.
A modell meghatározása
Azt az eseményt, hogy 2018. augusztus elsején délben egy golyó gurult végig egy vonal mentén, az asztalon, egy működő modell fogja szimulálni. A szimuláció kedvéért leegyszerűsítjük az eseményt. Feltételezzük, hogy a vonal tizenkilenc diszkrét helyből áll, és a valóságos időt a modell belső ideje szimulálja. Feltételezzük, hogy az idő véges, és tizenöt diszkrét idő atomból, röviden időpontból áll. A helyek és az időpontok rendezett halmazát természetes számok jelölik. Bármely nem utolsó időponthoz egyértelműen meghatározott a rákövetkező időpont, és bármely a szélsőtől eltérő helyhez meghatározott a két szomszédos hely. A modell belső világa tehát térben egydimenziós és minden téridő pontját egy számpár jelöli. Az ebben a világban lévő egyetlen objektumnak egyetlen tulajdonsága a világvonala, hogy melyik időpontban hol van. (Ez szimulálja a külső világban lévő golyót, amelyik végig gurul az asztalon egy vonal mentén.) Az objektum mozgása közben megtartja önazonosságát, egyazon objektum van különböző időpontokban különböző helyen. Az objektum minden időpillanatban egy és csak egy helyen van, amiből az következik, hogy az objektum vagy áll, vagy a maximális sebességgel időben előre halad, vagy átlagértékben lassabban halad. Ugyanis az álló állapot és a maximális sebesség időtartamának aránya átlagértékben megfelel különböző, a maximálistól lassabb sebességeknek. (Mindezek bizonyítása megtalálható más írásaimban.) A téren, időn és az objektumon kívül egyetlen természeti törvény érvényes ebben a véges világban, amelyik meghatározza az objektum világvonalát. Az objektum helyzetét meghatározó természeti törvény egyszerű formájú:
Az objektum t időpontban x helyen van pontosan akkor, ha Âxt. Az  relációt az alábbi 1. táblázat (mátrix) határozza meg (függőleges oszlop=idő, vízszintes sor=hely):
|
 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
11 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
14 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
- táblázat
Mint látható az  reláció függvény reláció, amelyik minden időponthoz meghatározza az objektum egyértelmű helyét. Az objektum bármely két helye között az összes közbenső helyen is áthalad, és soha nem lehet egyszerre két helyen.
A táblázatkezelő modell tulajdonságai a kibertérben
A táblázatkezelő modell két munkalapot tartalmaz. Az első, a ’present-dim’ nevű munkalap a működő modellt mutatja be. Ezen a munkalapon a modell a kibertér valóságában időben létezik, hasonlatosan ahhoz az eseményhez, ami a külső világban történt, és amit szimulál. A modell belső idejében az objektum az  relációnak megfelelő természeti törvény által előírt módon halad. A hatodik pozíciótól elmegy a nyolcadikig, ott rövid időre megáll, majd tovább megy a tizenegyedik pozícióig, ahol három ütemig áll. Ezután a tizenegyedig-pozícióig jut el, ahol visszafordul a tizenegyedik pozícióig. A második munkalap, a ’truth-dim’ ennek a piciny véges világnak a leírását tartalmazza grafikonok illetve egy propozíciót kifejező mondat formájában. A mondat szerint az objektum a második időpontban a hetedik helyen van, ami igaz. Figyeljük meg, hogy ez az igazság időtlen, miközben az első munkalapon az objektum mozog.
A táblázatkezelő modell innen tölthető le: http:// ferenc.andrasek.hu/models/time-series2.xlsx
A jelen modellje, az idő A teóriája
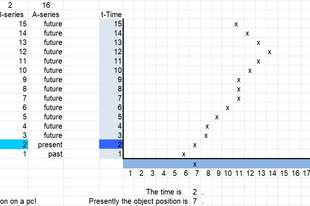
Az első, a ’present-dim’nevű munkalap ábrázolja az idő A teóriáját. 1. ábra azt a pillanatfelvételt ábrázolja, amikor az objektum a második időpillanatban a második helyen van. (Ennek megfelel, hogy a golyó az asztalon egy adott időpontban, egy adott helyen van.) A halványan sraffozott oszlop az időpontokat, az erősebben sraffozott oszlop a helyeket ábrázolja. Mind az időpontokat, mind a helyeket számokkal jelöltem, utóbbiak azonban a helyek alatt szerepelnek. Az objektumot az ’x’ jel képviseli, és az ábra mutatja, hogy éppen hol volt az objektum a pillanatfelvétel idején. Az időpontok egy sötétebb sávja mutatja a mindenkori jelent. Amennyiben a modellt kipróbáljuk, látni fogjuk, hogy az idő múlik, a jelen folyamatosan halad a jövő irányába, és az objektum mozog, azaz változtatja a helyét. Az erről készült pillanatfelvétel azonban statikus, nem jeleníti meg a mozgást és az idő múlását. Az objektum útvonalának megjelenítése természetes, ezzel szemben az idő jelenléte szokatlan. Szokatlan, hogy a modellben láthatóak mind a jövőbeli, mind a múltbeli időpontok, és a jelent jelképező sáv az objektum mindenkori helyzetéhez kapcsolódik, azzal van relációban. Valójában az oszlop egy lineáris óra, ahol a sraffozott sáv mutatja az időt. Mi a modellen kívüli valóságban hasonlóképpen látjuk az időt, amikor az órára nézünk, a különbség mindössze, hogy a mi óránk körbe jár.
Figure 1
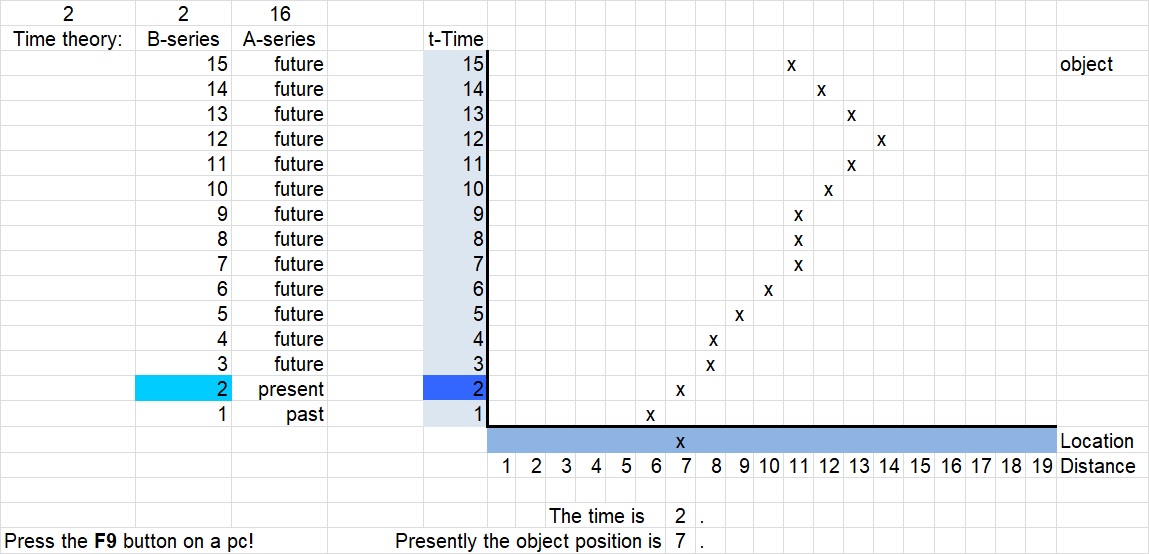
A modellben az idő gombnyomásra múlik. A gombnyomás a külső időben történik, a modell belső idejében két gombnyomás között az idő áll, megfagy a jelen. Ilyen módon közelebb kerülhetünk a jelen szemléléséhez, és megérhetjük rejtélyes természetét. Figyeljük meg a pillanatfelvétel alján lévő két mondatot. Az 1. Ábrán található két mondat nem azonos azzal, ami a munkalapon a kibertérben, időben létezik. Azért nem azonos, mert a kibertérben lévő mondat nem statikus létező, hanem folyamatosan változik az időben. A mondat a kibertérben megadja az objektum jelenbeli helyét és megadja, hogy mennyi az idő a modellen belül. Ezt a statikus szöveg világa képtelen visszaadni, csak egy pillanatnyi másolatát mutatja a modell belső valóságának, jelen esetben, hogy az idő kettő momentum, és most az objektum a hetedik helyen van. Ez a mondat azonban csak a pillanatfelvétel idején volt igaz, egy későbbi időpontban már hamissá válik, nincsen állandó, örök igazságértéke. A kibertérben a két mondat mindig igaz, mindig leírja, hogy, hány mennyi a (belső) idő és éppen hol van az objektum. Ez azonban a lehetetlen a statikus szöveg világában, azért képtelen ennek kifejezésére az idő B teóriája.
A jelen modellje, az idő B teóriája
A korábbi  reláció azt adta meg, hogy minden időpontban hol van az objektum. Ez a szemlélet nélkülözi a jelenre való utalást, nem más, mint az objektum mozgása leírása az idő B elméletében. Alább megmutatom, hogy ezen túl a modell segítségével mennyi fejezhető ki a ’jelen’ fogalmából az idő B teóriájában.
A második, a ’truth-dim’nevű munkalap ábrázolja az idő B teóriáját. A második, a ’truth-dim’ nevű munkalapon nem az időt és nem a helyet látjuk, hanem a neveiket. A második munkalapon lévő hely és időpont nevek az első munkalapon lévő helyekre és időpontokra utalnak. A nevek segítségével képesek vagyunk megadni igaz propozíciókat, sőt az objektum teljes világvonalát is leírhatjuk. Azt, hogy éppen hol van az objektum, azt képtelen kifejezni az idő B teóriája, de azt igen, hogy az összes lehetséges belső időpontban hol van az objektum. Erre olyan módon képes, hogy megadja az idő önmagára vonatoztatott relációjában a jelen grafikonját. A jelen grafikonja összes értéke pedig ábrázolja, hogy abban a jelenben éppen hol van az objektum, és abban a jelenben, mely állapotok voltak az objektum múltbeli, és melyek lesznek a jövőbeli állapotai. A 2. ábra tehát azt ábrázolja, hogy az idő függvényében melyik időpontban van a jelen, és akkor hol van az objektum.
Figure 2
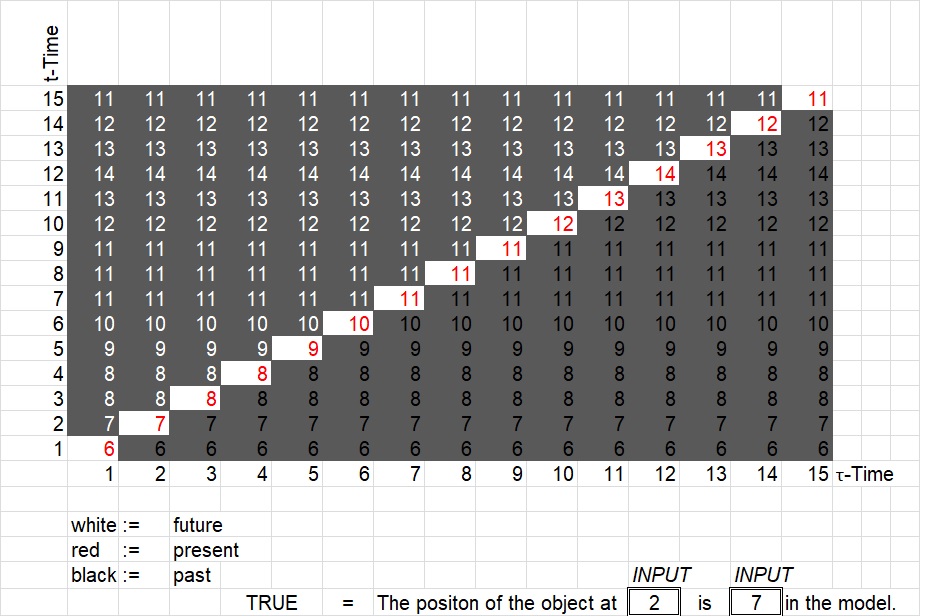
A 2. ábra alján lévő mondat igaz, és mindig igaz, mivel az idő B felfogásában gondolkozunk, ahol maguk az időbeli viszonyok statikusak, változatlanok. Ezért a 2. ábra alján lévő mondat propozíciót fejez ki, következésképpen joggal tulajdonítunk neki igazságértéket, mivel a mondat igazság értéke nem változik az időben.
A 2. táblázat egy kétváltozós függvényt ábrázol. A függvény azt mutatja meg, hogy az időpont-hely párokhoz a múlt, a jelen vagy a jövő tartozik-e. (Az előző mondatban a ’múlt, jelen, jövő’ idézőjelek nélkül szerepel, utalva arra, hogy a dolgokról és nem a neveikről beszélünk.) A függvény tehát az idő A teóriáját fogalmazza meg a propozíciók nyelvén, az igazság dimenziójában. Figyeljük meg, hogy minden időponthoz tartozik egy jelen, továbbá az objektum, amikor egy adott helyen van, akkor a jelenben van ott. Ezért az objektum létezése a modell belső idejében folyamatos.
|
távolság |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
jövő |
jövő |
jövő |
jövő |
jövő |
jövő |
jövő |
jövő |
jövő |
jövő |
jövő |
jövő |
jövő |
jövő |
jelen |
|
|
12 |
jövő |
jövő |
jövő |
jövő |
jövő |
jövő |
jövő |
jövő |
jövő |
jövő |
jövő |
jövő |
jövő |
jelen |
múlt |
|
|
13 |
jövő |
jövő |
jövő |
jövő |
jövő |
jövő |
jövő |
jövő |
jövő |
jövő |
jövő |
jövő |
jelen |
múlt |
múlt |
|
|
14 |
jövő |
jövő |
jövő |
jövő |
jövő |
jövő |
jövő |
jövő |
jövő |
jövő |
jövő |
jelen |
múlt |
múlt |
múlt |
|
|
13 |
jövő |
jövő |
jövő |
jövő |
jövő |
jövő |
jövő |
jövő |
jövő |
jövő |
jelen |
múlt |
múlt |
múlt |
múlt |
|
|
12 |
jövő |
jövő |
jövő |
jövő |
jövő |
jövő |
jövő |
jövő |
jövő |
jelen |
múlt |
múlt |
múlt |
múlt |
múlt |
|
|
11 |
jövő |
jövő |
jövő |
jövő |
jövő |
jövő |
jövő |
jövő |
jelen |
múlt |
múlt |
múlt |
múlt |
múlt |
múlt |
|
|
11 |
jövő |
jövő |
jövő |
jövő |
jövő |
jövő |
jövő |
jelen |
múlt |
múlt |
múlt |
múlt |
múlt |
múlt |
múlt |
|
|
11 |
jövő |
jövő |
jövő |
jövő |
jövő |
jövő |
jelen |
múlt |
múlt |
múlt |
múlt |
múlt |
múlt |
múlt |
múlt |
|
|
10 |
jövő |
jövő |
jövő |
jövő |
jövő |
jelen |
múlt |
múlt |
múlt |
múlt |
múlt |
múlt |
múlt |
múlt |
múlt |
|
|
9 |
jövő |
jövő |
jövő |
jövő |
jelen |
múlt |
múlt |
múlt |
múlt |
múlt |
múlt |
múlt |
múlt |
múlt |
múlt |
|
|
8 |
jövő |
jövő |
jövő |
jelen |
múlt |
múlt |
múlt |
múlt |
múlt |
múlt |
múlt |
múlt |
múlt |
múlt |
múlt |
|
|
8 |
jövő |
jövő |
jelen |
múlt |
múlt |
múlt |
múlt |
múlt |
múlt |
múlt |
múlt |
múlt |
múlt |
múlt |
múlt |
|
|
7 |
jövő |
jelen |
múlt |
múlt |
múlt |
múlt |
múlt |
múlt |
múlt |
múlt |
múlt |
múlt |
múlt |
múlt |
múlt |
|
|
6 |
jelen |
múlt |
múlt |
múlt |
múlt |
múlt |
múlt |
múlt |
múlt |
múlt |
múlt |
múlt |
múlt |
múlt |
múlt |
|
|
A |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
idő |
- táblázat
Futólagos megjegyzés a logikai determinizmusról
Ez egy teljesen determinisztikus modell, ahol az objektum helye bármelyik időpontban meghatározott a korábban megadott természeti törvény által, és azon túl, a természeti törvény egyszerűsége folytán könnyedén ábrázolhatjuk az objektum múltját és jövőjét, ahogy azt két ábra bemutatja. Valójában ebben a modellben az  reláció kettős szerepet játszik. Egyrészt előírja, meghatározza az objektum világvonalát, másrészt leírja, az objektum világvonalát (world line). Egy véletlenen alapuló modellben az objektum pályája nem előre meghatározott, azért a kettő nem esik egybe. Utólag a véletlen modellben is meghatározható az objektum pályája és az ennek megfelelő  reláció. De sztochasztikus modell esetén ez a reláció nem azonos az objektum viselkedését meghatározó természeti törvénnyel, mivel az pusztán valószínűségeket határoz meg. Előre nem ismerjük a véletlent használó modell esetén az  relációt, az azonban belátható, hogy a reláció létezik. A reláció létezése logikai-matematikai szükségszerűség, ami abból fakad, hogy a táblázat csak véges sok módon tölthető ki, és a kitöltések között lesz egy, amelyik leírja a jövőbeli történést. Hogy melyik azt viszont a véletlent használó modell esetén nem tudhatjuk előre.
A létezés dimenziói
Az e1 esemény csak egyetlen egyszer történt meg, ezzel szemben a róla készült film sokszor lejátszható. Hasonlóan a táblázatkezelő modellhez, amelyik szintén többször szimulálhatja a megtörtént e1 eseményt. A modell első munkalapja hasonlóan szimulálja a valóságos eseményt, a golyó gurulását, mintha filmre vettük volna az e1 eseményt. Mind a filmnek, mind a működő modellnek saját belső ideje van amelyik a külső időt hivatott leírni. A modell szimulál egy valóságos e1 eseményt olyan módon, hogy belülről nézve megjelenít egy véges világot az első, ’present-dim’ nevű munkalapon, és annak propozíciókkal történő leírását a második, a ’truth-dim’ nevű munkalapon. Amikor azonban a táblázatkezelő modell a valóságban működik, akkor kívülről nézve minden, amit látunk egyfajta létező a kibertérben. Kívülről nézve a táblázatkezelő modell puszta fizikai jelenség, ami az érzékszerveinkre hatva jelentést hordoz, gondolatot fogalmaz meg.
Táblázatban összefoglalva a lényeget:
|
Lét-dimenzió/ont. kategória |
Idő |
Fizikai tárgy |
Mennyiség |
… |
… |
|
Idő |
A teória |
Endurantizmus |
Jelpéldány |
|
|
|
Igazság |
B teória |
Perdurantizmus |
Szám |
|
|
Idő és igazság
Amíg a tudományos magyarázatokban az idő csak egy a lehetséges paraméterek közül, speciális folyamat, állapotok sorozata, melyhez más állapotokat, eseményeket, folyamatokat hozzárendelünk, addig a mindennapi életet átéljük az időben. Ezen a papíron egy teória található, mely időtlen, de amikor Ön olvassa, az egy történés, az élet része. Minden magyarázat egyben realitás is, de a papíroson létező tudomány nem vállalkozhat másra mint, hogy magyarázat legyen. A jelek nem mozdulnak meg a papíron, a kör egyenlete nem kerek, a mozgás matematikai leírása nem mozog, az idő leírása nem időbeli. Egy állítás igaz vagy hamis mivolta nem tett, csak kimondása teheti azzá, és egy helyesen gondolt gondolat sem lesz kimondott kizárólag igazsága folytán.
Egy elavult tudományos magyarázat a szaktudós számára értéktelen, míg a történész számára értékes lehet. Ez azért van így, mert a történész figyelme nem az állításokra, hanem az állításkimondásokra, azok körülményeire, keletkezésük magyarázatára irányul. A tudományos könyvek szólhatnak az időről, de a teória melyeket felállítanak ez esetben is időn kívüli. Egy kérdéskör története hasznos vagy egyenesen elengedhetetlen feltétele lehet a megértésnek, de a vita története sohasem érvényes érv a vita tárgyában. Az igazság nem történeti. A történeti (=idő) és a megismerés-tudomány (=igazság) dimenziója összeolvasztásának egyik esete volt az a marxista historizmus, amelyik egy történeti magyarázat egyedüli igazságának feltételezésével, a kérdések és válaszok, az elméleti problémák és magyarázataik megismerési dimenzióját beolvasztotta a történeti dimenzióba. Ezek után levezette a történelemből azt a választ, ami igazolta ama történeti levezetés helyességét, önmaga igazságát. Ezért az, hogy e teória, ha bármilyen elfajult formában is, de a valóságos és válságos történeti ágensek részévé vált, logikus következménye volt önmagának.
A körbeforgó gondolkozás nemcsak a teoretikus és történeti dimenzió összemosásának az esetén fordulhat elő, hanem a mindennapi és a megismerési dimenzió összemosásakor is. A hazug paradoxonhoz hasonló mondatok látszólag olyanok amikkel állítást tehetünk. Ha azonban ezt megkíséreljük, események olyan sorozatát kapjuk, ahol a mondat igazságértéke változó. Ugyanakkor a paradox mondatokat képesek vagyunk megérteni. Teljesen ellentmondásmentesen megértjük, hogy valahányszor igazságértéket tulajdonítunk ama nevezetes mondatnak, utána az ellenkezőjére kell következtessünk. Azért vagyunk erre képesek, és egyáltalán azért értjük meg a problémát, mert az időben kiterítve, az időben elmondva az antinómia leírható ellentmondásmentesen. Egy állítás megtételének a ténye is megváltoztathatja a világot, megváltoztathatja azt amiről az állítás szól, így akár ugyanaz a mondat többször elmondva más-más igazságfeltételekkel rendelkezhet pusztán csak attól, hogy már elhangzott. Megértjük a talányos mondatot, ha viszont valaki teljes komolysággal azt mondaná nekünk a telefonba, hogy „meglátogatlak és nem látogatlak meg”, akkor nem értenénk, hogy mit mond. A paradoxon viszont maga nem érthetetlen abban az értelemben, hogy arra szólít föl, oldd meg a problémát, keresed meg, hogy mi okozza az ellentmondást, és szüntesd meg a forrását!
Zárójeles befejező megjegyzés
Korábban háromdimenziósnak fogtam föl a létezést. Úgy gondoltam, hogy:
»… az egyén három dimenzióban éli az életét: mindennapi, történeti és teoretikus. Ezek a dimenziók, miként a tér síkjai, metszik egymást, és létünk egy vonal ebben a térben. A mindennapi élet ideje jelen idő, az átélt pillanat, a történelem ideje a jövő felé mutató múló idő, míg a megismerés, az igaz és hamis dimenziójának ideje egyfajta végtelenség, örökkévalóság. Az így kapott három dimenziónak és azok közötti relációnak, három nagy filozófiai irányzat felel meg: életfilozófiák, történelemfilozófiák és tudományfilozófiák. A három dimenzió vetülete a megismerés dimenziójában, mint sajátos nyelvfilozófia is megjelenik. A modern nyelvfilozófia egyik megalapítója írja iskola teremtő alapművében: „Először a mondás közben végrehajtott dolgok egy olyan csoportját különítettük el, amelyet összefoglalóan úgy jellemezhetünk, hogy lokúciós aktust végzünk. Ez nagyjából egyenértékű azzal, hogy valamely mondatot bizonyos értelemmel és jelölettel mondunk ki, ami viszont nagyjából egyenértékű a „jelentés” hagyományos értelmével. Másodszor azt mondtuk, hogy illokúciós aktusokat is végzünk, így tájékoztatunk, utasítunk, figyelmeztetünk, felvállalunk stb., vagyis a megnyilatkozásoknak van bizonyos (konvencionális) ereje. Harmadrészt megvalósítunk perlokúciós aktusokat is: akkor, amikor valaminek a mondása révén valósítunk meg vagy érünk el valamit, amikor meggyőzünk, elrettentünk vagy akár meglepünk vagy félrevezetünk valakit. Itt a „mondatok használatának” vagy a „nyelvhasználatnak” három, sőt több különböző értelméről, vagy ha úgy tetszik, dimenziójáról van szó …”. A megnyilatkozások lokúciós ereje, egyes mondatok ismeretközlő mivolta, az általuk kifejezett igaz vagy hamis propozíció, nem más, mint a megnyilatkozás vetülete a magyarázat, a megismerés dimenziójában; a megnyilatkozás cselekvő ereje, az illokúció, nem más, mint a megnyilatkozások megjelenése a mindennapi lét dimenziójában; a perlokúciós aspektus, a megnyilatkozások hatása, következménye, pedig nem más, mint a megnyilatkozás lenyomata a történeti dimenzióban.«
Nem tudom, hogy a két vagy háromdimenziós értelmezés szerencsésebb.
***
Korábbi posztok melyek a témához kapcsolódnak: 15, 16, 17, 32, 33, 56
A szöveg innen letölthető: http://ferenc.andrasek.hu/blog/pdf/a-letezes-dimenzioi.pdf

András Tibor: Tört képek