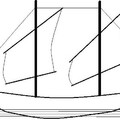
Képzeljünk el egy kertet, benne szép lombos fával. (Peter Strawson példája melyet Gallois említ a könyvben. A példát kissé módosítottam, ami a lényeget nem érinti. Occasions of identity, Introduction pp.2-4) A fának nyáron, egy adott t1 időpontban törzse és ágai is vannak. Ekkor jól láthatóan a törzs különbözik a belőle kinyúló ágaktól. A törzs valódi része a fának abban az értelemben, hogy a fához abban az időpontban a törzsön kívül más részek is tartoznak. Tehát t1 időpontban a fa nem azonos a törzsével. Ősszel a fa ágait levágták, és ezért egy adott őszi t2 időpontban a fa egy csupasz törzsből áll csupán. Szemmel látható, hogy ebben a későbbi időpontban a fa azonos a csupasz törzsével. Három fogalmunk van tehát: a fa, a fa törzse, a fa koronája, azaz a fa ágai. (A levelekkel most nem foglalkozunk.) A kérdés egyszerűen az, hogy mivel azonos a fa? Mindenekelőtt figyeljünk fül arra, hogy logikai-grammatikai szempontból a helyzet zavaros.
Az, hogy valami egy fa, logikai szempontból egy predikátum, viszont az a fa, amiről beszélünk, egy jól meghatározott egyedi dolog, amit a logika individuumnevekkel jelöl. Hasonló a helyzet a fa koronájával. Célszerű relációnak (többargumentumú predikátumnak) tekinteni azt, hogy y-koronája-x-fának-t-időpontban. De másképp is értelmezhetjük a relációt, mondhatjuk, hogy y-koronája-z-törzsnek-t-időpontban. Ekkor belátható, hogy:
(1) (y-koronája-x-fának-t-időpontban & y-koronája-z-törzsnek-t-időpontban) -> z-törzse-x-fának
Figyeljünk föl arra, hogy ha van egy egész, amit meghatározunk részei viszonyaival, akkor az utóbbi meghatározás fölöslegessé teszi az egész fogalmát. Jelen esetben ez azt jelenti, hogy a ’fa’ fogalma fölösleges, a ’törzs’ neve és a ’koronája’ reláció helyettesíteni tudja. Fontos észben tartani a következő összefüggéseket is:
(2) (y-koronája-x-fának-t-időpontban & z-törzse-x-fának) -> y-koronája-z-törzsnek-t-időpontban
(3) x-fa-tömege-t1-időpontban >< x-fa-törzse-tömege-t1-időpontban (mivel ekkor a fának van koronája)
(4) x-fa-árnyéka-t1-időpontban >< x-fa-törzse-árnyéka-t1-időpontban (mivel ekkor a fának van koronája)
(5) x-fa-átmérője-t1-időpontban >< x-fa-törzse-átmérője-t1-időpontban (mivel ekkor a fának van koronája)
A példák a fa és a fa törzse közötti különbségről folytathatóak. Ezeket majd a későbbiekben fogjuk hasznosítani. Gallois szerint a következő természetes hiteink vannak a fákról és részeikről. (7-8 oldal)
(6.1) A fák, törzseik és az őket alkotó molekulák léteznek.
(6.2) Valójában mind a fák mind a törzseik semmi másból nem állnak, mint molekulákból, azaz azonosak molekulák egy összességével (collection). Molekulák különböző összessége van a fa és a törzs térben elfoglalt helyén.
(6.3) A korábbi fa azonos a molekulák egy összességével.
(6.4) A korábbi időszakban a fa törzse is azonos a molekulák egy összességével.
(6.5) A korábbi időszakban a molekulák két csoportja létezik.
(6.6) Az egyedi dolgok a fa (növény), a korábbi törzs (szár) és a molekulás összessége.
Gallois szerint öt féle módon gondolkozhatunk az felmerült azonossági kérdésről.
(i) David Wiggins szerint sem a fa sem a törzse nem azonos az azokat alkotó molekulák összességével. Az azonosság másfajta viszony mint az alkotás. Molekulák alkotják a fákat, de a fák nem azonosak a molekulákkal. Mind a korábbi (t1), mind a későbbi (t2) időpontban a fa különbözik a törzsétől. De ez hogyan egyeztethető össze azzal, hogy később a fa megkülönböztethetetlen a törzsétől? Korábban a fa nem csak a törzséből állt, később viszont igen.
(ii) Roderick Chisholm álláspontja más. A fák és törzseik nem élik túl a változásokat. A korábbi fa azonos egy bizonyos molekulák összességével, a későbbi fa más molekulák összességével. A fa nem testesít meg önálló fajtát, csak molekulák összességeként létezik. Mind a fa mind a törzse azonos a molekulák összességével. A korábbi fa azonos a törzs és ágak együttesével a későbbi viszont csak a törzzsel, tehát a korábbi és a későbbi fa nem azonosak egymással. A későbbi fa azonos a puszta törzzsel. De akkor miképpen érthető az a mondat, hogy a fának később hiányoznak az ágai? Hiszen nem ugyanarról a fáról beszélünk, a későbbi fának sosem voltak ágai.
(iii) Peter van Inwagen úgy látja a korábbi fa azonos a későbbi fával, és a későbbi törzs azonos a későbbi fával. Ugyanakkor a későbbi törzs nem azonos a korábbi törzzsel, sőt valójában a törzs nem is létezett amikor még koronája is volt, azaz amikor még valódi része volt a fának. A koronás fának szerinte nem valódi része a törzse. Ebből a nézetből az következik, hogy a későbbi törzs azonos a korábbi fával, amelyiknek van koronája. De akkor a kettőnek eltérőek a tulajdonságai, az egyiknek van koronája, míg a másiknak nincsen. Ez hogyan lehetséges összhangban Leibniz törvényével?
(iv) Mind a törzs mind a fa időben kiterjedt négydimenziós objektumok. Ezeknek a különböző időszeletei eltérő fa és törzs időbeli részek, melyek nem azonosak egymással. Ugyanakkor a törzs és a fa egy bizonyos későbbi időtartományban – amikor csupasz a törzs – egybe esik. Ezzel a megközelítéssel több baj van. A fizikai tárgyak perdurantista felfogása filozófiai problémák megoldására jó, alkalmas a nevek jelölete magyarázatára, de a filozófiai problémák megoldásán túl használhatatlan, nem is használja sem a köznapi élet, sem a tudomány, sem azon belül pl. az objektum orientált programozási nyelvek világa.
(v) Ez a legkülönösebb értelmezés. A korábbi fa azonos a későbbi fával, ám a korábbi és a későbbi törzse különböző, nem azonos. A korábbi és a későbbi törzs megegyezik, de nem egyazon növény részeiként.
Gallois szerint (v) sem nem csökkenti, sem nem szaporítja a létezők számát. A fa és a törzs viszonya megfelel természetes elvárásainknak. A természetes hitek halmaza koherens. Az objektumok többszörözése helyett az azok közötti relációkat többszörözi meg. Nem egyetlen azonosság reláció van ebben a felfogásban, hanem több.
Gallois szerint a kézenfekvő értelmezés az volna, hogy a fa és törzse korábban különböztek, míg később azonossá váltak. Ez az felfogás szerinte a (iv) és (v) értelmezéssel van összhangban. Szerinte Leibniz törvénye tart vissza minket attól, hogy ezt az azonosság értelmezést elfogadjuk.
Gallois szerint a példa mutatja, hogy az azonosság klasszikus logikai értelmezése ellentmond a fizikai tárgyak időbeli azonosságának. Én nem így gondolom. Az én megoldásom a következő. Kvázi formalizált nyelvet használok, remélhetőleg az olvasó könnyebbségére. Jelen esetben már ezzel az nyelvvel is kiküszöbölhetőek a köznapi nyelvhasználat filozófiai használatából fakadó zavarok.
A jelenség leírása:
(7.1) Koronája-van(fa,t1) & Nincs-koronája(fa,t2)
(7.2) Koronája-van(törzs,t1) & Nincs-koronája(törzs,t2)
(7.3) Nincs-kornája(fa,t2) & Nincs-koronája(törzs,t2)
(7.4) Koronája-van(fa,t1) & Koronája-van(törzs,t1)
A fa minden időpontban kicsiny részek (pl. molekulák) meghatározott struktúrája, amit relációkkal írhatunk le. A koronás fa t1 időpontban:
(8.1) fa[t1]= <A,R>
A fa törzse ugyanekkor
(8.2) törzs[t1]= <T,R’> ahol R’ egy másik, szűkebb reláció.
Mivel a törzs valódi része a fának, ezért az előbbi molekulái részhalmaza az utóbbi molekuláinak. Hasonló igaz a viszonyokat leíró relációkra is. Mindezt formális nyelven így írhatjuk le:
(8.3) TÌ A és R’Ì R következésképpen T><A és R’><R
A koronájától megfosztott fa t2 időpontban egy még újabb R’’ reláció:
(8.4) fa[t2]= <T,R’’> ahol R’’><R
A fa törzse ugyanekkor ettől megkülönböztethetetlen:
(8.5) törzs[t2]= <T,R’’>
A fentiek alapján belátjuk, hogy:
(9.1) fa[t1] >< fa[t2] (8.1)(8.4)mivel az előbbin van korona az utóbbin nincsen
(9.2) törzs[t1] >< törzs[t2] (8.2)(8.5)mivel az előbbin van korona az utóbbin nincsen
(9.3) fa[t2]= törzs[t2] (8.4)(8.5) mivel az azonosság szemmel látható
Ezekből az következi, hogy:
(9.4) fa[t1] >< törzs[t2] (8.1)(8.4)
Feltevésünk szerit mind a fa mind a törzs időbeli példányai összességével azonos:
(9.5) fa={…fa[t1],…fa[t2]…}
(9.6) törzs={…törzs[t1],…törzs[t2]…}
Ebből az következi, hogy:
(9.7) fa >< törzs (9.5) (9.6) (9.4) Halmazelmélet
Ezzel igazoltuk, hogy a fa nem azonos a törzsével, még akkor sem, ha bizonyos időszakaszban megkülönböztethetetlenek. Ezt alátámasztja az is, hogy
(9.8) tömege(fa) >< tömege(törzs) -> fa >< törzs
A fa időbeli önazonosságával kapcsolatos filozófiai rejtvény megoldása az, hogy alkalmazni kell a formális logika nyelvét.