„Mi az igazság” kérdezte Pilátus a Mestert, de meg sem várta a választ, mert nem hitt az igazságban. Rosszul tette.[i]
Tudni való, hogy az emberi mondatokat három zsákban gyűjti az Úristen. Jobb keze mellett vannak az igaz kijelentő mondatok, balján a hamisak, míg a bizonytalan vagy zavaros értelműek a középső zsákba kerülnek. Valamennyi mondat egy papírszeletre kerül, és katonás rendben minden papírszeleten egy jel van, olyan gondosan, hogy semelyik mondat nem marad ki a jelölésből, és nincs két mondat azonos jellel ellátva, továbbá minden mondat csak egyszer fordul elő. Nem hagyja az Úr, hogy az angyalok tétlenül lóbálják a lábukat a felhők szélén. Bambulás helyett az a dolguk, hogy a középső zsákból kivegyék a homályos értelmű mondatokat, és értelmező megjegyzésekkel ellátva megpróbálják azokat szilárd, világos jelentéssel ellátni. Mikor ez sikerül nekik, a mondat ismét az Úristen színe elé kerül, aki a megfelelő jobb vagy baloldali zsákba helyezi a javított mondatot.
Történt egyszer, hogy Lucifer borsot akart törni az atya orra alá, és azért a következő mondatot csempészte az angyalok elé:[ii]
(λ) Ez az λ-jelű mondat, amit olvasol, összezavar, nem találsz fogást rajta, mert nem igaz vagy igazsága bizonytalan, vagy talán nincs is neki.
Az angyalok elolvasták a cetlit, megértették az abban foglaltakat, hiszen teljesen világos hogy miről szól ez a mondat. Az ördög mondata önmagáról szól. De nem azt állítja, hogy hány betűből áll, vagy hogy milyen nyelven íródott, hanem az igazságáról állít valamit. Valami furcsát, szokatlant mond, ami egyszerűnek és teljesen érthetőnek tűnik, vagy talán valóban az is. Már csak az a kérdés, hogy melyik zsákba kerüljön? Az angyalok néhanapján szerényen odaírták a javaslatukat a cetli hátoldalára, de ez esetben vitatkozni kezdtek egymással, olyan hangosan veszekedtek, hogy fölébresztették a trónusán szunyókáló atyát, aki feddőleg megintette őket: „Ne veszekedjetek, hozzátok csak elém azt a mondatot, majd én eldöntöm a kérdést. Ha valóban teljesen érthető és egyértelmű, amit a mondat mond, akkor bizonyosan vagy igaz, vagy hamis, harmadik eset nem lehetséges.” Így gondolkozott. A mondat igazsága a tényektől függ, és tény az, hogy nem egyértelmű a mondat igazsága, tehát úgy van ahogy mondja. Márpedig ha a valóság úgy van ahogy a mondat mondja, akkor az a mondat igaz, tehát az λ nevű mondat igaz. Várjunk csak, mielőtt betesszük a jobboldali zsákba, hogy is van ez? Ha az λ nevű mondat igaz, akkor úgy van ahogy mondja. Márpedig azt mondja, hogy nincs neki vagy csak bizonytalanul van igazsága, márpedig a jobboldali zsákban csak olyan teljesen bizonyos igazságok vannak, mint, hogy „A hó fehér”. Ez a mondat nem ilyen, tehát nem kerülhet a jobboldali zsákba. Akkor pedig a baloldali zsákba kell kerüljön, a hamisak közé, mert bizonyos van értelme ennek a mondatnak, csak egy kicsit becsapós. Tehát nem igaz, hogy ez a mondat, amit olvasol, összezavar, nem találsz fogást rajta, mert nem igaz vagy igazsága bizonytalan, vagy talán nincs is neki. Már majdnem a következő mondat után nézett az Úr, amikor meghallotta Lucifer kuncogását. Újra elgondolkozott. Ha ez a mondat hamis, akkor egyértelmű igazságértéke van, biztos, hogy nem igaz. Ha viszont nem igaz, akkor miképpen lehet, hogy amit a mondat mond megfelel a tényeknek: nem igaz vagy igazsága bizonytalan … Az igazsága nem bizonytalan, viszont a vagy kapcsolat másik fele teljesül, nevezetesen, hogy a mondat nem igaz. Ekkor pedig maga a mondat egésze is igaz kell legyen, és nem pedig hamis. Ellentmondásba keveredtünk, de most már világos a helyzet: a mondat se nem igaz, se nem hamis, hanem merő értelmetlenség, zűrzavar, és ez bizonyosság. Hoppá, a mondat épp ezt állítja, tehát igazat mond, akkor mégiscsak igaz. Ezt azonban már egyszer megvizsgáltuk, kezdhetjük előröl, ördögi körbe kerültünk. Ekkor azonban fölnézett az Úr a trónusa fölé és csendesen elmosolyodott.
 A dolog úgy történt, hogy ide érkezett egy bizonyos Alfred Tarski nevű lélek, aki egyszer a mennyországbeli villásreggelinél amint Cantorral és Russellal beszélgetett halkan megjegyezte, hogy nincs az jól, hogy az atyának csak három zsákra telik. Építsünk neki végtelen sok emeletet a trónusa fölé végtelen sok zsákkal. Georg te hozod az alapanyagot a végtelen sok emelethez, Bertrand, te pedig alkosd meg a szinteket. Így is lett. Amikor az atyának eszébe ötlött, hogy az első emeleten lévő zsákokban olyan mondatok vannak, melyek a földszinti mondatokról szólnak, a második emeleten pedig azok, melyek az első emeleten lévő mondatokról, egy laza mozdulattal földobta Lucifer mondatát egy emelettel följebb az egyik zsákba. Ezt látva Lucifer leforrázva elsomfordált. Miért érezte legyőzve magát a gonosz szellem? Most akkor Lucifer mondata igaz vagy sem? Lehet erre egyáltalán meggyőző választ adni, mi az igazság? Röviden elmagyarázom.
A dolog úgy történt, hogy ide érkezett egy bizonyos Alfred Tarski nevű lélek, aki egyszer a mennyországbeli villásreggelinél amint Cantorral és Russellal beszélgetett halkan megjegyezte, hogy nincs az jól, hogy az atyának csak három zsákra telik. Építsünk neki végtelen sok emeletet a trónusa fölé végtelen sok zsákkal. Georg te hozod az alapanyagot a végtelen sok emelethez, Bertrand, te pedig alkosd meg a szinteket. Így is lett. Amikor az atyának eszébe ötlött, hogy az első emeleten lévő zsákokban olyan mondatok vannak, melyek a földszinti mondatokról szólnak, a második emeleten pedig azok, melyek az első emeleten lévő mondatokról, egy laza mozdulattal földobta Lucifer mondatát egy emelettel följebb az egyik zsákba. Ezt látva Lucifer leforrázva elsomfordált. Miért érezte legyőzve magát a gonosz szellem? Most akkor Lucifer mondata igaz vagy sem? Lehet erre egyáltalán meggyőző választ adni, mi az igazság? Röviden elmagyarázom.
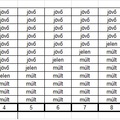
Lucifer λ nevű mondata L1 emberi nyelv része. Az Úr ezt a mondatot a szeráfok nyelvén, eggyel magasabb szintű L2 nyelven értékeli ki. Ezen a magasabb szintű nyelven használjuk az ’igaz1’ és ’hamis1’ metanyelvi (szemantikai) predikátumokat, melyek terjedelmébe a tárgynyelv mondatai tartoznak, így ide tartozik Lucifer (λ) nevű mondata is. A nyelvi szintekre utal a szemantikai predikátumok indexe. Metanyelvi szinten λ sem nem igaz1 sem nem hamis1. Tehát L2 nyelven – halmazelméleti nyelvet használva – azt állítja az Úr, hogy, λ∉igaz1 és λ∉hamis1. Utóbbi mondat neve, egy még magasabb szintű L3 nyelven μ. (μ='λ∉igaz1 és λ∉hamis1') L3 nyelven definiált ’igaz2’ fogalom szerint, az Úr μ nevű mondata igaz2, ami természetes, hiszen az Úr mindig igazat mond. Foglaljuk össze mindezt egy táblázatban:
|
Nyelv |
Mondat |
Metanyelvi értékelés |
|
L1 |
Ez az λ-jelű mondat, amit olvasol, összezavar, nem találsz fogást rajta, mert nem igaz vagy igazsága bizonytalan, vagy talán nincs is neki. |
Nincs igazság1-értéke |
|
L2 |
Lucifer mondata sem nem igaz1 sem nem hamis1. |
Igaz2 |
|
L3 |
Igaz2 az, hogy Lucifer mondata sem nem igaz1 sem nem hamis1. |
Igaz3 |
|
… |
… |
… |
Tarski koncepciójában minden n nyelvi szinten érvényes az a (T) kritérium, hogy ha egy n-1 szinten megfogalmazott p mondat neve n nyelvi szinten x, akkor és csak akkor x-igazn-1- n nyelvi szinten, ha p. Másképp mondva, x-igazn-1- n nyelvi szinten, pontosan akkor, ha úgy van, ahogy az x nevű mondat mondja. Lényeges, hogy visszafelé is érvényes a tétel, tehát ha azt állítjuk, hogy p, és p neve x, akkor x-igaz. Az igazság fogalma meghatározása formális nyelven, formálisan korrekt és materiálisan adekvát módon kell legyen kidolgozva; másképp mondva következnie kell belőle az összes (T) formájú ekvivalenciának. Ruzsa Imre megjegyzi, hogy Tarski koncepciója olyan formában is megfogalmazható, hogy az igazság hordozói kijelentések (propozícók) és nem (bizonyos egyértelmű információ tartalommal rendelkező, időtlen igazságértékű) mondatok.[iii] Kripke, Barwise vagy Belnap és mások újabb igazság elméletei más igazság fogalmat definiálnak, így ezek nem cáfolatai, hanem alternatívái Tarski elméletének. A poszt szövege innen letölthető.
[i] A szöveg rövidebb formában korábban megjelent a Namitgondolsz.hu blogon.
[ii] A Milétoszi Eubulidész, Epimenidész, Alfred Tarski és Ruzsa Imre nyomán.
[iii] Alfred Tarski, Bizonyítás és igazság (1990) Gondolat, Bp., pp 74-78 szerkesztői kommentár. Megjegyzem, hogy a könyv 69. oldalán téves az az állítás, hogy ‘(A<-->p)-->~p’ formula ekvivalens ’~A’-val. Valójában ez csak akkor igaz, ha p=A. Ettől függetlenül a Tarski által fölismert ellentmondás létezik.