Előhang

1977. október 25-én beküldtem egy pár oldalas írást a Magyar Filozófiai Szemlének, amelyik a hazug paradoxont tárgyalta új megközelítésben. Azt állította, hogy a paradoxon logikai szerkezete hasonlít az egyszerű villanycsengő működéséhez. A csengő karja akkor van meghúzva, ha előtte nem volt, és fordítva, ha nincs meghúzva, akkor a következő időpontban egyet kondul a csengő. Meglepő módon Kéri Elemér professzornak tetszett az ötletem, de azt javasolta, hogy egészítsem ki a probléma történetének bemutatásával és magyarázzam el jobban, akkor leközlik. Engem azonban kevéssé érdekelt a probléma története, és sajnos nem tudok – azóta sem tudok – jól magyarázni, olyanoknak beszélek érthetően, akik maguk is hasonlókat gondoltak. Írásomat megmutattam Ruzsa Imre professzornak is, aki figyelmesen elolvasta, de tévesnek, alapvetően elhibázottnak találta. Adott nekem egy mindössze egy oldalas tömör megjegyzést arról, hogy Tarski szellemében hogyan kellene helyesen kezelni az igazsággal kapcsolatos filozófiai-logikai problémákat. Megéreztem, hogy valamit nem értek kellő mélyen, és ezért egy ideig nem foglalkoztam tovább a problémával. De hiába olvastam el úja és újra Ruzsa megjegyzését, nem értettem. Pontosabban minden szavát értettem, csak a lényeget nem. Azóta számos felületes, sőt alapvetően elhibázott vagy egyenesen hajmeresztő értelmezését olvastam Tarski igazság elméletének, még jelentős, neves filozófusok részéről is. Csaknem húsz év múlva értettem meg a Tarski féle igazság felfogás logikai-filozófiai lényegét, és most már értem egykori tanárom megjegyzését, látom, hogy igaza volt. Ugyanakkor az évek során a probléma nem hagyott nyugodni, újra és újra megfogalmaztam az ötletemet, mindig egy kicsit másképp. Több írásom is tárgyalta a szemantikai paradoxonokat, olyan is volt, ami megjelent. Most újra nekifutok.

I. A probléma bemutatása

Saul Kripke említi nagy hatású tanulmányában a következő tanulságos ellenpéldát.[i] Hogyan értékeljük az igazságérték szempontjából az alábbi megnyilatkozásokat, ahol Jones (c2) és (c6) mondatot, Nixon pedig a (c3), (c4) és (c5) mondatokat állította:

Jones ezeket mondta:

(c2) Nixon Watergate-ügyről tett nyilatkozatainak többsége (több mint a fele) hamis.

Ezen kívül Jones a ’mondat6’ mondatot mondta, melynek neve (c6), igazságértéke b6.

Nixon ezeket mondta:

(c3) Jones minden Watergate-ügyről tett állítása igaz.

Ezen kívül Nixon a ’mondat4’ és ’mondat5’ mondatokat állította, ezek nevei rendre (c4) és (c5), igazságértékei b4 és b5. A három független mondat (mondat4, 5 és 6) sem direkt sem közvetve nem vonatkozik a történet szereplői mondataira, azaz nem utal sem (c2)-re sem (c3) ra.

Tekintsük rögzítettnek, hogy melyik mondatot mondta Jones és melyiket Nixon. Így az is rögzített, hogy Nixon állította a ‘mondat4’ és ‘mondat5’ mondatokat, míg a ‘mondat6’ mondatot Jones mondta. Táblázattal így ábrázolhatjuk, hogy melyik mondatot ki mondta:

táblázat 1

II. Az értékelés alapgondolata

A (c4), (c5) és (c6) mondatoknak az értékelése független tény, nem függ sem Jones, sem Nixon semelyik mondatától. Figyeljük meg, mind (c2) mind (c3) mondat használja az ’igaz’ vagy a ’hamis’ predikátumot, és mindkét mondat igazságértéke valamilyen módon a másik igazságértékétől is függ. Ezek alapján a (c2) és (c3) mondatok igazságértéke csak és kizárólag a ’mondat4, mondat5 és mondat6’ mondatok igazságértékétől, illetve a (c2) és (c3) mondat kölcsönösen egymásra való hivatkozásától függ. A mondatok közül azonban kizárólag a ’mondat4, mondat5 és mondat6’ állításokat értékelhetjük szabadon, a (c2) és (c3) mondatokat nem. A (c2) és (c3) mondatok igazságértéke valahogy következik a mások három értékeléséből, bár még nincsen módszerünk annak pontos meghatározására. Annyi belátható, hogy (c4), (c5) és (c6) mondatok igazságértékei határozzák meg, hogy van-e, és mi az igazságértéke Jones (c2) és Nixon (c3) mondatának. Ez összesen nyolc variációt jelent, a következőkben valamennyi esetet megvizsgáljuk. A kérdés az, hogy milyen nyelven és milyen eszközökkel tehetjük meg ezt? Hogyan tudjuk Jones (c2) és Nixon (c3) mondata igazságértékét meghatározni? Vizsgáljuk ezt meg közelebbről.

Nixon szerint Jones minden mondata igaz. Mivel Jonesnak összesen két mondata van, ezért Nixon az alábbit állítja: Jones minden Watergate-ügyről tett állítása igaz pontosan akkor, ha Nixon Watergate-ügyről tett nyilatkozatainak többsége (több mint a fele) hamis és ’mondat6’ igaz. A jelölések fölhasználásával jobban látjuk a logikai kapcsolatokat.

Nixon:  (c3)-igaz pontosan akkor ha (c2)-igaz és (c6)-igaz

Jones komplikáltabb állítást tett Nixon mondatairól. Szerinte Nixon mondatainak többsége hamis. Nixon három mondatot mondott. Csak úgy lehet ezek többsége hamis, ha legfeljebb egyetlen igaz a háromból. De mi van akkor, ha nem csak a többsége, hanem Nixon valamennyi állítása hamis? Mi a helyzet, ha Jones (c6) mondata is hamis? Milyen módon lehet valamennyi lehetőséget kiszámítani? Milyen nyelven lehet a feladatot úgy megfogalmazni, hogy könnyen számba vehessük az összes eshetőséget? Az alábbi táblázat összefoglalja az eddigieket és bemutatja a következőkben alkalmazott mondat értékeléseket. A táblázat jobb oldali oszlopában e2 X b2 =1 ha b2 igaz és Jones állította c2 mondatot, e3 X b3 = 1 ha b3 igaz, és Jones állította c3 mondatot, stb.; a második sorban b3 = 1, pontosan akkor, ha a Jones által állított valamennyi mondat igaz. Nixon mondatainak száma e9.

táblázat 2

III. A klasszikus felfogás korlátai

Alfred Tarski alapvető belátásait követve, nincsen vezérfonalunk abban az irányban, hogy a Jones által használt igazság fogalmat helyezzük el az első metanyelvi szinten, és a Nixon által használt igazság fogalmat eggyel feljebb, egy második metanyelvi szinten, vagy éppen fordítva. Az ugyanis nyilvánvaló, hogy mivel mindkét igazságfogalom terjedelmébe beletartozik a másik igazság predikátum egy alkalmazása, a két metanyelvi igazság predikátum nem lehet egyazon metanyelvi szinten. Ezt méltán hangsúlyozza Kripke ama nevezetes tanulmányában. A Tarksi által megrendszabályozott formális nyelven a fenti érvelés, a nyelv keretei között, annak részeként, valamilyen Tarskiánus igazságfogalmat alkalmazva meg sem fogalmazható. Ebben is igaza van Kripkének. (Az más kérdés, hogy ez a korlátja a klasszikus felfogásnak erény-e vagy hiba? Szerintem erény.) Abban viszont sem Kripkének, sem másoknak, akik alternatív igazság koncepciót dolgoztak ki, nincsen igaza, hogy a szokásos Tarskiánus logika felfogásában maga a jelenség, ahogy a szemantikai paradoxonok megjelennek, ne lenne leírható. Ebben az esetben a paradoxont jelenségként, egyfajta esemény sorozatként fogjuk fel, és nem pedig egy helyesnek tekintett logikai nyelv keretei között megfogalmazott érvelésként.  A következőkben több féle modellt is bemutatok, ahol a modellek viselkedése szimulálja azt a jelenséget, amikor szemantikai paradoxonokba ütközünk. Tehát nem egy újabb formális nyelvet konstruálok, hanem modelleket, melyekkel metanyelvi szinten, szemantikai értékelő függvényeket alkalmazva, de a klasszikus logika keretei között maradva írom le a jelenséget. A modellek szimulálják a szemantikai jelenséget. A modellek nem az ’igaz’ és ’hamis’ szavakat használják, hanem az ezeknek megfelelő ’1’ és ’0’ jelsorozatokat. Némelyik esetben az ’1’ és ’0’ számjelek puszta karakterek, más esetben számokat jelentenek. Utóbbi eset akkor ár fenn, amikor aritmetikai függvényekkel kapcsolatban használom azokat.

IV. Aritmetikai transzformáció

Tetszőleges s mondat igazságértékét |s| jelöli. A ζ függvény az igazságértékekhez számokat rendel, az hamishoz a nullát, az igazhoz az egyet.

(4.1) c2 pontosan akkor ha 0,5 > (ζ|c3| + ζ|c4| + ζ|c5|) /3

(4.2) c3 pontosan akkor ha c2 és c6

(4.3) c2 pontosan akkor ha 0,5 > (ζ|c2| X ζ |c6| + ζ|c4| + ζ|c5|) /3

Bevezetve a kézenfekvő definíciókat: b2:= ζ|c2|; b3:= ζ|c3|; b4:= ζ|c4|; b5:= ζ|c|; b6:= ζ|c6|; ezt kapjuk.

(4.4) b2 = ζ|0,5 > (b2 X b6 + b4 + b5) /3)|

Az egyenlet legegyszerűbben táblázatkezelő programok alkalmazásával oldható meg, melynek segítségével az alábbi igazságtáblázatot kapjuk. Emlékeztetünk arra, hogy b2 Jones mondta értéke, és b3 Nixon mondata értéke, ahol b2 ismeretében b3 könnyen kiszámolható: b3 = b2 X b6 Ahol nincsen megoldás – nincs fix pont – ottan a táblázatkezelő nem ad állandó értéket, hanem ingadozik a 0 és 1 értékek között.

táblázat 3

V. Véges automata modell

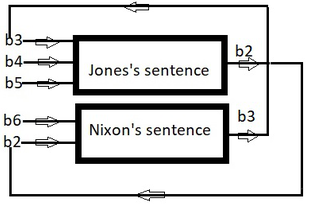
Az 1. ábra mutatja, hogy a mondatok összefüggéseit digitális áramkörök összefüggéseivel is szimulálhatjuk. Az ábra szerint az áramkörök kimeneti állapota önmagától is függ. A visszacsatolás az igazság értékek cirkularitását szimulálja. Az ilyen visszacsatolt áramköröket sorrendi hálózatoknak nevezik, mert működésük nem írható le egyszerűen a bemeneti jelek függvényeként. Leírásukra nem alkalmas az igazság függvények nyelve, más matematikai eszközre van szükségünk. 

ábra 1

A korábbiak alapján elkészítjük a probléma Mealy féle véges automata szimulációját. Az automata kimenete Jones és Nixon mondata értéke, bemenete a többi mondat értéke. Az automatának két belső állapota van, melyek a mondatok értékelése szituációit szimulálják.

(5.1) kimenet = λ(bement, belső állapot)

(5.2) következő belső állapot = δ(bement, belső állapot)

(5.3) belső állapot (szituáció) = {0,1}

(5.4) bemenet = <b6, b5, b4> azaz a három mondat.

(5.5) kimenet = <b2, b3> azaz Jones és Nixon mondata

Az automata működését – a δ és λ függvényeket – a 4. és 5. táblázat határozza meg.

táblázat 4, 5

A véges automata modell a kibertérben működik is, és bármely bemenetre megadja a kimeneti értéket. Amelyik bemenetre nincsen megoldása a problémának, azaz ahol ellentmondásba keveredünk (nincs fix pont), ottan az automatának nincsen stabil (állandósult) állapota és felváltva ingadozik az 1 (igaz) és 0 (hamis) állapot között. Ilyen módon a hazug paradoxon többféle verziója is szimulálható véges automaták segítségével. A szemantikai értékek véges automata működéssel történő szimulálása azokban az esetekben alkalmazható, ahol a tárgyalási univerzum véges. A működő modellek innen letölthetőek:

<url=http://ferenc.andrasek.hu/models/kripke-s-counterexample.xls>

<url=http://ferenc.andrasek.hu/models/liar-models.xls>

A poszt szövege innen letölthető.

[i]“Most (i.e., a majority) of Nixon's assertions about Watergate are false. …Everything Jones says about Watergate is true.” Saul Kripke, "Outline of a Theory of Truth" (1975) The Journal of Philosophy, Vol. 72, No. 19, p. 691. Megtalálható a neten, de benne van a Robert L. Martin által szerkesztett "Recent Essays on Truth and the Liar Paradox" könyvben OUP 1984, pp. 53-81. Legújabb munkájában visszatér a kérdéshez: “Ungroundedness in Tarskian Languages”, Journal of Philosophical Logic, 2018 october 25, pp 1 -7. Tarski írásai "Bizonyítás és igazság" címmel jelentek meg 1990-ben. Jon Barwise és John Etchemendy "Liar" c. könyve szintén alapműve a témának.  Anil Gupta és Nuel Belnap "The Revision Theory of Truth" c. könyve sajátos felfogást mutat be. A klasszikus felfogással kapcsolatban érdemes elolvasni Quine The Ways of Paradox c. könyvét is.